已知抛物线y2=2px(p>0)的焦点为F,点P是抛物线上的一点,且其纵坐标为4,|PF|=4.
(Ⅰ)求抛物线的方程;
(Ⅱ) 设点A(x1,y1),B(x2,y2)(yi≤0,i=1,2)是抛物线上的两点,∠APB的角平分线与x轴垂直,求△PAB的面积最大时直线AB的方程.
【答案】
分析:(I)根据抛物线的定义,利用|PF|=4,求得P即可;
(II)根据条件判定直线PA、PB的斜率关系,求出直线AB的斜率,再设出直线AB的方程,根据三角形PAB面积最大时的条件,求出三角形PAB面积的最大值,
及最大值时直线AB的方程.
解答:解:(I)∵|PF|=4,∴x
P+
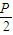
=4,
∴P点的坐标是(4-
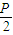
,4),
∴有16=2P(4-
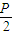
)⇒P=4,
∴抛物线方程是y
2=8x.
(II)由(I)知点P的坐标为(2,4),
∵∠APB的角平分线与x轴垂直,∴PA、PB的倾斜角互补,即PA、PB的斜率互为相反数,
设PA的斜率为k,则PA:y-4=k(x-2),k≠0
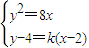
⇒
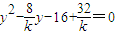
,方程的解为4、y
1,
由韦达定理得:y
1+4=
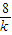
,即y
1=
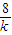
-4,同理y
2=-

-4,
k
AB=
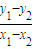
=
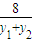
=-1,
设AB:y=-x+b,
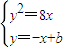
⇒y
2+8y-8b=0,
由韦达定理得:y
1+y
2=-8,y
1y
2=-8b,
|AB|=
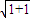
|y
1-y
2|=8
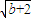
,点P到直线AB的距离d=
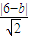
,
S
△ABP=2
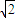
×

,设b+2=t
则(b+2)(b
2-12b+36)=t
3-32t-64-(3t-8)(t-8),
∵△=64+32b>0⇒b>-2,y
1•y
2=-8b≥0⇒b≤0,∴-2<b≤0,
设t=b+2∈(0,2],
则(b+2)(b
2-12b+36)=t
3-16t
2+64t=f(t),
f
′(t)=3t
2-32t-64=(3t-8)(t-8),
由t∈(0,2]知f
′(t)>0,∴f(t)在(0,2]上为增函数,
∴f(t)
最大=f(2)=72,
∴△PAB的面积的最大值为2
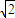
×
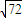
=24,
此时b=0,直线AB的方程为x+y=0.
点评:本题考查直线与圆锥曲线的关系及抛物线的标准方程.

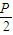 =4,
=4,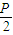 ,4),
,4),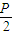 )⇒P=4,
)⇒P=4,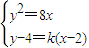 ⇒
⇒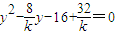 ,方程的解为4、y1,
,方程的解为4、y1,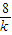 ,即y1=
,即y1=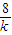 -4,同理y2=-
-4,同理y2=- -4,
-4,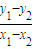 =
=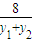 =-1,
=-1,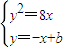 ⇒y2+8y-8b=0,
⇒y2+8y-8b=0,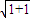 |y1-y2|=8
|y1-y2|=8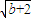 ,点P到直线AB的距离d=
,点P到直线AB的距离d=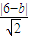 ,
,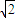 ×
× ,设b+2=t
,设b+2=t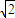 ×
×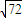 =24,
=24,
