
(本小题满分12分)
已知函数f(x)=" cos(" 2x+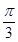 )+sin2x.
)+sin2x.
(Ⅰ)求函数f(x)的最小正周期和值域;
(Ⅱ)在△ABC中,角A、B、C的对边分别为a、b、c,满足
2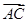 ·
·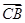 =
=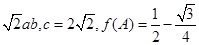 , 求△ABC的面积S.
, 求△ABC的面积S.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
(本小题共12分)
已知△ABC的角A,B,C的对边依次为a,b,c,若满足 ,
,
(1)求∠C大小;
(2)若c=2,且△ABC为锐角三角形,求a+b取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)  =(
=( ),
),  =
= ,f(x)=
,f(x)=
①求f(x)图象对称中心坐标
②若△ABC三边a、b、c满足b2=ac,且b边所对角为x,求x的范围及f(x)值域。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
(理)某种型号汽车四个轮胎半径相同,均为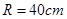 ,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为
,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为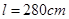 (假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路
(假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路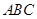 (如图(1)所示,其中
(如图(1)所示,其中 (
( )),且前轮
)),且前轮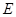 已在
已在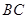 段上时,后轮中心在
段上时,后轮中心在 位置;若前轮中心到达
位置;若前轮中心到达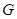 处时,后轮中心在
处时,后轮中心在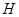 处(假定该汽车能顺利驶上该上坡路). 设前轮中心在
处(假定该汽车能顺利驶上该上坡路). 设前轮中心在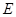 和
和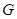 处时与地面的接触点分别为
处时与地面的接触点分别为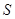 和
和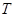 ,且
,且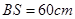 ,
,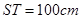 . (其它因素忽略不计)
. (其它因素忽略不计)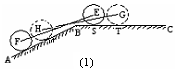
(1)如图(2)所示,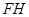 和
和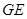 的延长线交于点
的延长线交于点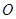 ,
,
求证: (cm);
(cm);
(2)当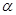 =
=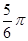 时,后轮中心从
时,后轮中心从 处移动到
处移动到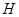 处实际移动了多少厘米? (精确到1cm)
处实际移动了多少厘米? (精确到1cm)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)在△ABC中,角A、B、C所对的边分别为a、b、c,向量 =
= ,
, =(cos2A,2sinA),且
=(cos2A,2sinA),且 ∥
∥ .
.
(1)求sinA的值;
(2)若b=2,△ABC的面积为3,求a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com