
(本题满分13分)在△ABC中,角A、B、C所对的边分别为a、b、c,向量 =
= ,
, =(cos2A,2sinA),且
=(cos2A,2sinA),且 ∥
∥ .
.
(1)求sinA的值;
(2)若b=2,△ABC的面积为3,求a.
(1)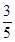 ;(2) 当cosA=
;(2) 当cosA=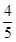 时, a=
时, a=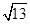 ;当cosA=-
;当cosA=-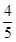 时, a=3
时, a=3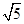 。
。
解析试题分析:(1)∵ ∥
∥ ,∴
,∴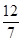 cos2A=(1-sinA)·2sinA, 3分
cos2A=(1-sinA)·2sinA, 3分
∴6(1-2sin2A)=7sinA(1-sinA)⇒5sin2A+7sinA-6=0,
∴sinA=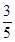 或sinA=-2(舍去). 6分
或sinA=-2(舍去). 6分
(2)由S△ABC= bcsinA=3,b=2,sinA=
bcsinA=3,b=2,sinA=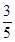 ,得c=5, 8分
,得c=5, 8分
又cosA=±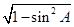 =±
=±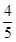 ,
,
∴a2=b2+c2-2bccosA=4+25-2×2×5cosA=29-20cosA, 10分
当cosA=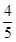 时,a2=13⇒a=
时,a2=13⇒a=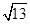 ;
;
当cosA=-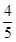 时,a2=45⇒a=3
时,a2=45⇒a=3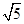 . 13分
. 13分
考点:数量积;向量共线的条件;余弦定理;三角形的面积公式。
点评:本题是一个三角函数同向量结合的问题,是以向量平行条件,得到三角函数的关系式,是一道综合题,在高考时可以选择和填空形式出现,也可以作为解答题的一部分出现。


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数f(x)=" cos(" 2x+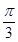 )+sin2x.
)+sin2x.
(Ⅰ)求函数f(x)的最小正周期和值域;
(Ⅱ)在△ABC中,角A、B、C的对边分别为a、b、c,满足
2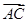 ·
·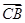 =
=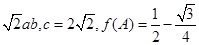 , 求△ABC的面积S.
, 求△ABC的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com