Question

13．已知矩形ABCD中，$AB=\sqrt{2}$，BC=1，则$\overrightarrow{AC}•\overrightarrow{DB}$=（　　）

• A． 1
• B． -1
• C． $\sqrt{6}$
• D． $2\sqrt{2}$

Answer 1

分析 法一、以A为坐标原点，AB为x轴，AD为y轴建立平面直角坐标系，得到点的坐标，进一步求得向量$\overrightarrow{AC}、\overrightarrow{DB}$的坐标得答案；
法二、以$\overrightarrow{AB}、\overrightarrow{AD}$为基底，把$\overrightarrow{AC}、\overrightarrow{DB}$用基底表示，则$\overrightarrow{AC}•\overrightarrow{DB}$可求．

解答 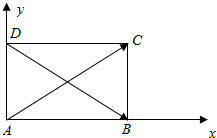解：法一、如图，
以A为坐标原点，AB为x轴，AD为y轴建立平面直角坐标系，
则A（0，0），$B（\sqrt{2}，0）$，$C（\sqrt{2}，1）$，D（0，1），
∴$\overrightarrow{AC}=（\sqrt{2}，1）$，$\overrightarrow{DB}=（\sqrt{2}，-1）$，
则$\overrightarrow{AC}•\overrightarrow{DB}=2-1=1$．
故选：A．
法二、记$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AD}=\overrightarrow b$，
则$\overrightarrow a•\overrightarrow b=0$，$|{\overrightarrow a}|=\sqrt{2}$，$|{\overrightarrow b}|=1$，
∴$\overrightarrow{AC}•\overrightarrow{DB}=（\overrightarrow a+\overrightarrow b）•（\overrightarrow a-\overrightarrow b）$=${\overrightarrow a^2}-{\overrightarrow b^2}=2-1=1$．
故选：A．

点评 本题考查平面向量的数量积运算，解答此类问题常用两种方法，即建系法或利用平面向量基本定理解决，建系法有时能使复杂的问题简单化，是中档题．