
 sinx+
sinx+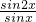
 ,求
,求 的最大值.
的最大值. sinx+
sinx+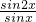 =2
=2 sinx+2cosx=4sin(x+
sinx+2cosx=4sin(x+ )
) =2kπ+
=2kπ+ (k∈Z)时,f(x)取得最大值为4
(k∈Z)时,f(x)取得最大值为4 ,k∈Z}.
,k∈Z}. )=1
)=1
 =cbcosA=
=cbcosA=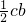

 的最大值
的最大值 ,此时b=c=
,此时b=c=
 =cbcosA=
=cbcosA=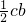 ,结合余弦定理及基本不等式可求最值
,结合余弦定理及基本不等式可求最值

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 8 |
| π |
| 8 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省温州市八校联考高三(上)期初数学试卷(文科)(解析版) 题型:解答题
 倍,
倍,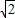 倍,
倍,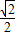 倍,
倍, 个单位,⑧向右平移
个单位,⑧向右平移 个单位,
个单位, 个单位,⑩向右平移
个单位,⑩向右平移 个单位,
个单位,查看答案和解析>>
科目:高中数学 来源:2013年河北省石家庄一中高考数学一模试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
科目:高中数学 来源:2012年河北省石家庄市高考数学一模试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com