
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
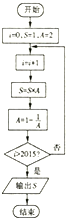
分析 模拟程序框图的运行过程,得出该程序是以6为周期的计算S值的循环程序,结合i的值即可得出结果.
解答 解:模拟程序框图的运行过程,得;
i=0,S=1,A=2;
i=1,S=1×2=2,A=1-$\frac{1}{2}$=$\frac{1}{2}$;
i=2,S=2×$\frac{1}{2}$=1,A=1-2=-1;
i=3,S=1×(-1)=-1,A=1+1=2;
i=4,S=-1×2=-2,A=1-$\frac{1}{2}$=$\frac{1}{2}$;
i=5,S=-2×$\frac{1}{2}$=-1,A=1-2=-1;
i=6,S=-1×(-1)=1,A=1+2=2;…;
∴该程序是以6为周期的计算S值的循环程序;
∴当i=2016=336×6时,S=1,A=2,终止循环;
即该程序运行后输出的是S=1.
故选:B.
点评 本题考查了利用循环结构求数值的应用问题,解题时应根据框图的流程判断算法的功能,是基础题目.


科目:高中数学 来源: 题型:解答题
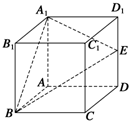 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{40}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
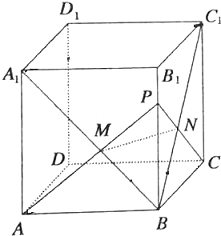 如图,在长方体ABCD-A1B1C1D1中,点P∈BB1(P不与B,B1重合).PA∩A1B=M,PC∩BC1=N.
如图,在长方体ABCD-A1B1C1D1中,点P∈BB1(P不与B,B1重合).PA∩A1B=M,PC∩BC1=N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com