
���� ��1�����������нǹ�ʽ���ɵó���
��2���������������������ʡ��������߶������ɵó���
��� �⣺��1����$\overrightarrow a$��$\overrightarrow b$�ļн�Ϊ�ȣ���$cos��=\frac{4��1+3����-1��}{{\sqrt{{4^2}+{3^2}}\sqrt{{1^2}+{{��-1��}^2}}}}=\frac{{\sqrt{2}}}{10}$����$\overrightarrow a$��$\overrightarrow b$�ļнǵ�����ֵΪ$\frac{\sqrt{2}}{10}$��
��2����$\overrightarrow a$=��4��3����$\overrightarrow b$=��1��-1����
��$3\overrightarrow a+4\overrightarrow b=��12��9��+��4��-4��=��16��5��$��$��\overrightarrow a-\overrightarrow b=��4�ˣ�3�ˣ�-��1��-1��=��4��-1��3��+1��$��
������$3\overrightarrow a+4\overrightarrow b$��$��\overrightarrow a-\overrightarrow b$ƽ�У�
��16��3��+1��=5��4��-1����
���$��=-\frac{3}{4}$��
���� ���⿼���������нǹ�ʽ�����������������ʡ��������߶�����������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6��2.4 | B�� | 6��5.6 | C�� | 2��5.6 | D�� | 2��2.4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
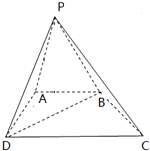 ��ͼ������P-ABCD�ĵ�����ֱ�����Σ�AB��CD��AB��AD����PAB�͡�PAD�������߳�Ϊ2���������Σ�DC=4��
��ͼ������P-ABCD�ĵ�����ֱ�����Σ�AB��CD��AB��AD����PAB�͡�PAD�������߳�Ϊ2���������Σ�DC=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2 | 3 | 5 | 7 | 8 |
| A�� | 1.6 | B�� | 2.6 | C�� | 3.6 | D�� | 4.6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{69}{56}$ | B�� | $\frac{7}{8}$ | C�� | $\frac{69}{28}$ | D�� | $\frac{7}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��A��B��CΪ��O�����㣬BΪ$\widehat{AC}$���е㣬PΪAC�ӳ�����һ�㣬PQ���O�����ڵ�Q��BQ��AC�ཻ�ڵ�D��
��ͼ��A��B��CΪ��O�����㣬BΪ$\widehat{AC}$���е㣬PΪAC�ӳ�����һ�㣬PQ���O�����ڵ�Q��BQ��AC�ཻ�ڵ�D���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com