
| A. | m>-4 | B. | m<-4 | C. | m>-5 | D. | m<-5 |
分析 将不等式两边都除以x,变形整理得:m>$\frac{-{x}^{2}-4}{x}$=-(x+$\frac{4}{x}$)令f(x)=-(x+$\frac{4}{x}$),m应大于f(x)的最小值.
解答 解:不等式x2+mx+4>0即为不等式-x2-4<mx,因为x在(1,2)上,所以m>$\frac{-{x}^{2}-4}{x}$=-(x+$\frac{4}{x}$)令f(x)=-(x+$\frac{4}{x}$),
则f(x)在(1,2)上单调递增,所以f(x)∈(f(1),f,(2))=(-5,-4),
不等式x2+mx+4>0有解,只需m>-5
故选C.
点评 本题考查不等式的意义和参数取值范围,考查转化计算,逻辑思维能力.本题的易错点在于判断不出m应大于f(x)的最小值.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 496 | B. | 33 | C. | 31 | D. | $\frac{31}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数段 | [0,7) | [7,8) | [8,9) | [9,10] |
| 个数 | 1 | 3 | 8 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
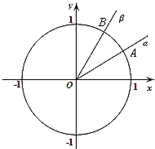 如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f({x_1})<\frac{3+2ln2}{4}$ | B. | $f({x_1})<-\frac{1+2ln2}{4}$ | C. | $f({x_1})>\frac{1+2ln2}{4}$ | D. | $f({x_1})>-\frac{3+2ln2}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com