练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数 ，的导函数为.

    （1）讨论函数的单调区间；

    （2）对于曲线上的不同两点，，，求证：在内存在唯一的，使直线的斜率等于.

    【答案】(1)a＞0时， 上单调递增，在上单调递减.时在（0，+∞）单调递减. (2)见证明

    【解析】

    （1）对a分两种情况讨论，利用导数求函数的单调区间；（2）即 只需证明，且唯一．再构造函数证明得解.

    解：（1），

    又的定义域为

    当时，函数在区间上单调递减；

    当时，

    该函数在上单调递增，在上单调递减.

    （2）∵，

    ∴，化简得

    即

    因此，要证明原命题成立，只需证明

    ，且唯一．

    设， ①

    则，

    再设，，

    ∴，

    ∴在是增函数，

    又，∴ ②

    同理 ③

    ∵一次函数在上是增函数，

    因此由①②③得在有唯一解，

    故原命题成立．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，点在椭圆上.

    (1)求椭圆的方程；

    (2)若不过原点的直线与椭圆相交于两点，与直线相交于点，且是线段的中点，求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在几何体中，四边形为菱形，对角线与的交点为，四边形为梯形， .

    （Ⅰ）若，求证： 平面；

    （Ⅱ）求证：平面平面；

    （Ⅲ）若， ， ，求与平面所成角.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图①，在直角梯形ABCD中，AD＝1，AD∥BC，AB⊥BC，BD⊥DC，点E是BC边的中点，将△ABD沿BD折起，使平面ABD⊥平面BCD，连接AE，AC，DE，得到如图②所示的几何体.

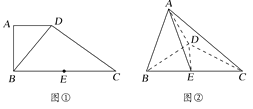
    (1)求证：AB⊥平面ADC；

    (2)若AC与平面ABD所成角的正切值为，求二面角B—AD—E的余弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系O中，直线与抛物线＝2相交于A、B两点．

    （1）求证：命题“如果直线过点T（3，0），那么＝3”是真命题；

    （2）写出（1）中命题的逆命题，判断它是真命题还是假命题，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设,分别为椭圆:的左右焦点,已知椭圆上的点到焦点,的距离之和为4.

    (1)求椭圆的方程;

    (2)过点作直线交椭圆于,两点,线段的中点为,连结并延长交椭圆于点(为坐标原点),若,,等比数列,求线段的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】长方形中， ， 是中点（图1）．将△沿折起，使得（图2）在图2中：

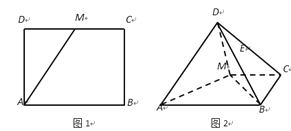
    （1）求证：平面 平面；

    （2）在线段上是否存点，使得二面角为大小为，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中，四边形为平行四边形， 　平面，且是的中点.

    （1）求证： 平面；

    （2）求二面角的余弦值的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关……”其大意为：“某人从距离关口三百七十八里处出发，第一天走得轻快有力，从第二天起，由于脚痛，每天走的路程为前一天的一半，共走了六天到达关口……” 那么该人第一天走的路程为______________

    查看答案和解析>>

    同步练习册答案