练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)＝ln x，g(x)＝x2－4x＋4，则方程f(x)－g(x)＝0的实根个数是 (　　)．

    A．0 B．1 C．2 D．3

     

    C

    【解析】由f(x)－g(x)＝0，得f(x)＝g(x)．

    在同一坐标系内作出函数y＝f(x)与y＝g(x)的图象，

    由图知f(x)，g(x)的图象有两个交点．

    因此方程f(x)－g(x)＝0有两个不相等的实根．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-5-1练习卷（解析版） 题型：解答题

    如图所示是一几何体的直观图、正(主)视图、侧(左)视图、俯视图．

    (1)若F为PD的中点，求证：AF⊥面PCD；

    (2)求几何体BEC－APD的体积．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-3-2练习卷（解析版） 题型：选择题

    已知sin 2α＝，则cos2 ＝ (　　)．

    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-2-3练习卷（解析版） 题型：选择题

    已知函数f(x)＝x(ln x－ax)有两个极值点，则实数a的取值范围是(　　)．

    A．(－∞，0) B．(0，) C．(0,1) D．(0，＋∞)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-2-2练习卷（解析版） 题型：解答题

    设函数f(x)＝ax2＋bx＋b－1(a≠0)．

    (1)当a＝1，b＝－2时，求函数f(x)的零点；

    (2)若对任意b∈R，函数f(x)恒有两个不同零点，求实数a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-2-1练习卷（解析版） 题型：解答题

    已知二次函数f(x)＝ax2＋bx＋1(a>0)，F(x)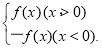＝若f(－1)＝0，且对任意实数x均有f(x)≥0成立．

    (1)求F(x)的表达式；

    (2)当x∈[－2,2]时，g(x)＝f(x)－kx是单调函数，求k的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-2-1练习卷（解析版） 题型：选择题

    函数y＝的图象大致是 (　　)．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-1-2练习卷（解析版） 题型：填空题

    已知两个单位向量a，b的夹角为60°，c＝ta＋(1－t)b.若b·c＝0，则t＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习真题感悟选修4练习卷（解析版） 题型：填空题

    如图，AB为圆O的直径，PA为圆O的切线，PB与圆O相交于D.若PA＝3，PD∶DB＝9∶16，则PD＝________，AB＝________.

     

     

    查看答案和解析>>

    同步练习册答案