已知等差数列{an}的首项为a,公差为b,等比数列{bn}的首项为b,公比为a,n=1,2,…,其中a,b均为正整数,且a1<b1<a2<b2<a3.
(Ⅰ)求a的值;
(Ⅱ)若对于{an},{bn},存在关系式am+1=bn,试求b的值;
(Ⅲ)对于满足(Ⅱ)中关系式的am,试求a1+a2+…+am.
解:(I)由题设知,a
n=a+(n-1)b,
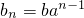
(1分)
由已知可得,a<b<a+b<ab<a+2b
∴b<ab,a>1(2分)
∴ab<a+2b<3b又∵b>0
∴a<3(3分)
∵a为正整数
∴a=2(4分)
(II)a
m+1=b
n,可得a+(m-1)+1=b•a
n-1(5分)
∵a=2
∴3+(m-1)b=b•2
n-1则
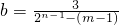
(6分)
∵b>a=2且b为正整数∴2
n-1-(m-1)=1(7分)
∴b=3(8分)
(III)由(II)知,m=2
n-1,a
n=3n-1
∴a
1+a
2+…+a
m=(3•1-1)+(3•2-1)+…(3•2
n-1-1)(9分)
=
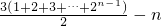
=
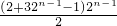
(11分)
=3•2
2n-3+2
n-2(12分)
分析:(I)由题设可求,a
n,b
n,结合已知a
1<b
1<a
2<b
2<a
3.可得a<3,由a为正整数可求a
(II)由a
m+1=b
n,a=2可求得
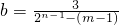
,由b>a=2且b为正整数 可求
(III)由(II)知,m=2
n-1,a
n=3n-1,代入a
1+a
2+…+a
m=(3•1-1)+(3•2-1)+…(3•2
n-1-1),利用分组求和,结合等差数列的求和公式可求
点评:本题主要考查了等差数列与等比数列的通项公式的应用,求和公式的应用,解答本题还要求考生具备一定的综合应用知识的能力

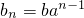 (1分)
(1分)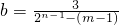 (6分)
(6分)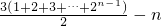
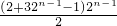 (11分)
(11分)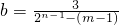 ,由b>a=2且b为正整数 可求
,由b>a=2且b为正整数 可求

 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.