
| 22(1-41007) |
| 1-4 |


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
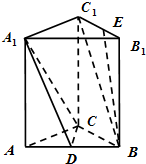 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=BB1,点D是AB的中点,
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=BB1,点D是AB的中点,
| ||
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 成都七中学生会经过综合考评,新招了14名男生和6名女生到学生会工作,茎叶图表示这20名同学的测试成绩(单位:分),规定:成绩在180分以上者到“M部门”工作;成绩在180分以下者到“N部门”工作.
成都七中学生会经过综合考评,新招了14名男生和6名女生到学生会工作,茎叶图表示这20名同学的测试成绩(单位:分),规定:成绩在180分以上者到“M部门”工作;成绩在180分以下者到“N部门”工作.查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| π |
| 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com