
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
| 1 |
| 2 |
| 1 |
| 1+an |
| 1 |
| 1+a1 |
| 1 |
| 2k-1 |
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
| 1 |
| 2 |
| 1 |
| 1+an |
| 1 |
| 1+a1 |
| 1 |
| 2k-1 |
| n |
 |
| k=1 |
| 1 |
| 1+ak |
| 1 |
| 1+a1 |
| 1 |
| 1+a1 |
| n |
 |
| k=2 |
| 1 |
| 2k-1 |
| 1 |
| 1+a1 |
| n |
 |
| k=1 |
| 1 |
| 2k-1 |
| 2 |
| 1+a1 |
| 2 |
| 1+3 |
| 1 |
| 2 |
| 1 |
| 1+a1 |
| 1 |
| 1+a2 |
| 1 |
| 1+an |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
| A、x与y有关系,犯错的概率不超过1% |
| B、x与y有关系,犯错的概率超过1% |
| C、x与y没有关系,犯错的概率不超过1% |
| D、x与y没有关系,犯错的概率超过1% |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、{x|0<x<1} |
| B、{x|0<x≤1} |
| C、{x|1≤x<2} |
| D、{x|2≤x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:
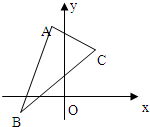 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).查看答案和解析>>
科目:高中数学 来源: 题型:
| n+2 |
| n |
| an |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
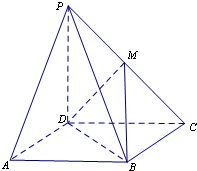 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 在某文艺会场中央有一块边长为a米(a为常数)的正方形地面全彩LED显示屏如图所示,点E,F分别为BC,CD边上异于点C的动点.现在顶点A处有视角∠EAF=45°的摄像机,正录制移动区域△ECF内表演的某个文艺节目.设DF=x米,BE=y米.
在某文艺会场中央有一块边长为a米(a为常数)的正方形地面全彩LED显示屏如图所示,点E,F分别为BC,CD边上异于点C的动点.现在顶点A处有视角∠EAF=45°的摄像机,正录制移动区域△ECF内表演的某个文艺节目.设DF=x米,BE=y米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com