分析:建立空间直角坐标系后,设PB
1=t,在AC
1上任取一点Q,要使△APC
1的面积S最小,必有
⊥与
⊥,
求点P,Q的坐标后,即可求出三角形高的最小值,由此可求S的最小值.
解答:解:以D
1为原点,D
1A
1为x轴,D
1C
1为y轴,D
1D为z轴建立空间直角坐标系,
设PB
1=t(0<t<1),则A(1,0,1),C
1(0,1,0),P(1,1,t),在AC
1上任取一点Q(a,b,c),
由
=λ,得(a-1,b,c-1)=λ(-1,1,-1),
∴a=1-λ,b=λ,c=1-λ,
令x=1-λ,有Q(x,1-x,x),又
=(-1,1,-1),
=(0,0,1),
=(x-1,-x,x-z),
当△APC
1的面积S的最小时,
||最小,必有
⊥,
⊥,
得
,∴
| | (x-1,-x,x-t)•(-1,1,-1)=0 | | (x-1,-x,x-t)•(0,0,1)=0 |
| |
⇒,
解得
x=t=,这时
||=
|(-,-,0)|=,即
||≥,又
||=.
∴△APC
1的面积
S=||•||≥,即△APC
1的面积S的最小值为
.
点评:本题考点是点、线、面间的距离的计算,由于本题易于建立空间直角坐标系求距离,进而求△APC1的面积,所以选用了“坐标法”,但要注意过程中的细节处理,尽一切可能的降低运算量,如令x=1-λ.若用“几何法”,易产生漏洞,因位置关系判断不准而致求△APC1的面积出错.

 如图,已知正方体ABCD-A1B1C1D1的棱长为1,点P在棱BB1上运动(不含B,B1两点),求△APC1的面积S的最小值.
如图,已知正方体ABCD-A1B1C1D1的棱长为1,点P在棱BB1上运动(不含B,B1两点),求△APC1的面积S的最小值. 

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )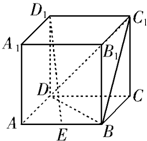 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.