
【题目】数列{an}满足Sn=2n-an(n∈N*).
(1)计算a1,a2,a3,a4,并由此猜想通项公式an;
(2)用数学归纳法证明(1)中的猜想.
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】
(1)当n=1时,a1=S1=2-a1,∴a1=1.当n=2时,a1+a2=S2=2×2-a2,∴a2=![]() .
.
当n=3时,a1+a2+a3=S3=2×3-a3,∴a3=![]() .
.
当n=4时,a1+a2+a3+a4=S4=2×4-a4,∴a4=![]() .
.
由此猜想![]() (n∈N*).
(n∈N*).
(2)证明:①当n=1时,a1=1,结论成立.
②假设n=k(k≥1且k∈N*)时,结论成立,即![]() ,
,
那么n=k+1(k≥1且k∈N*)时,
ak+1=Sk+1-Sk=2(k+1)-ak+1-2k+ak
=2+ak-ak+1.∴2ak+1=2+ak=2+![]() =
=![]() .
.
∴ak+1=![]() ,由①②可知,对n∈N*,
,由①②可知,对n∈N*,![]() 都成立.
都成立.


科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AB=1,BC=2,AC![]() ,PC
,PC![]() ,PA
,PA![]() ,PB
,PB![]() ,E是线段BC的中点.
,E是线段BC的中点.
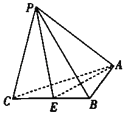
(1)求点C到平面APE的距离d;
(2)求二面角P﹣EA﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据中点坐标公式求出![]() 中点
中点![]() 的坐标,根据斜率公式可求得
的坐标,根据斜率公式可求得![]() 的斜率,利用点斜式可求
的斜率,利用点斜式可求![]() 边上的中线所在直线的方程;(2)先根据斜率公式求出
边上的中线所在直线的方程;(2)先根据斜率公式求出![]() 的斜率,从而求出
的斜率,从而求出![]() 边上的高所在直线的斜率为
边上的高所在直线的斜率为![]() ,利用点斜式可求
,利用点斜式可求![]() 边上的高所在直线的方程.
边上的高所在直线的方程.
试题解析:(1)由B(10,4),C(2,-4),得BC中点D的坐标为(6,0),
所以AD的斜率为k=![]() =8,
=8,
所以BC边上的中线AD所在直线的方程为y-0=8(x-6),
即8x-y-48=0.
(2)由B(10,4),C(2,-4),得BC所在直线的斜率为k=![]() =1,
=1,
所以BC边上的高所在直线的斜率为-1,
所以BC边上的高所在直线的方程为y-8=-(x-7),即x+y-15=0.
【题型】解答题
【结束】
17
【题目】已知直线l:x-2y+2m-2=0.
(1)求过点(2,3)且与直线l垂直的直线的方程;
(2)若直线l与两坐标轴所围成的三角形的面积大于4,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:![]() ,经统计,其高度均在区间
,经统计,其高度均在区间![]() ,
,![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图.其中高度为
分成6组,制成如图所示的频率分布直方图.其中高度为![]() 及以上的树苗为优质树苗.
及以上的树苗为优质树苗.

(1)求图中![]() 的值,并估计这批树苗的平均高度(同一组中的数据用该组区间的中点值作代表);
的值,并估计这批树苗的平均高度(同一组中的数据用该组区间的中点值作代表);
(2)已知所抽取的这120棵树苗来自于![]() ,
,![]() 两个试验区,部分数据如下列联表:
两个试验区,部分数据如下列联表:
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有![]() 的把握认为优质树苗与
的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由.
两个试验区有关系,并说明理由.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据7至11月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,参考数据:
,参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(Ⅰ)证明MN∥平面PAB;
(Ⅱ)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】F是双曲线![]() 1(a>0,b>0)的左焦点,过点F作双曲线的一条渐近线的垂线,垂足为A,交另一条渐近线于点B.若3
1(a>0,b>0)的左焦点,过点F作双曲线的一条渐近线的垂线,垂足为A,交另一条渐近线于点B.若3![]() ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )
A.2B.3C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com