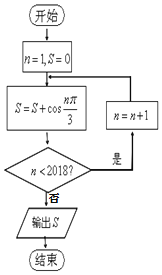
【题目】运行如图所示的程序框图，则输出的结果S为（ ）
A. 
B. 
C. 0D. 
【答案】C
【解析】
执行如图所示的程序框图，得到s的值呈周期性变化，且周期为6，进而可求解输出的结果，得到答案.
模拟执行程序框图，可知：
n=1，S=0+
=；
满足条件n＜2018，执行循环，n=2，S=-=0；
满足条件n＜2018，执行循环，n=3，S=0-1=-1；
满足条件n＜2018，执行循环，n=4，S=-1-=-
；
满足条件n＜2018，执行循环，n=5，S=-+=-1；
满足条件n＜2018，执行循环，n=6，S=-1+1=0；
满足条件n＜2018，执行循环，n=7，S=0+=；
满足条件n＜2018，执行循环，n=8，S=-=0；
…
观察规律可知，S的值以6为周期循环，而2018=336×6+2，
所以输出S=0．
故选：C．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知圆C：x2+y2+2x﹣2y+1＝0和抛物线E：y2＝2px（p＞0），圆C与抛物线E的准线交于M、N两点，△MNF的面积为p，其中F是E的焦点．
（1）求抛物线E的方程；
（2）不过原点O的动直线l交该抛物线于A，B两点，且满足OA⊥OB，设点Q为圆C上任意一动点，求当动点Q到直线l的距离最大时直线l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高校随机抽取部分男生测试立定跳远，将成绩整理得到频率分布表如表，测试成绩在220厘米以上（含220厘米）的男生定为“合格生”，成绩在260厘米以上（含260厘米）的男生定为“优良生”．
分组（厘米） | 频数 | 频率 |
[180，200） | 0.10 | |
[200，220） | 15 | |
[220，240） | 0.30 | |
[240，260） | 0.30 | |
[260，280） | 0.20 | |
合计 | 1.00 |
（1）求参加测试的男生中“合格生”的人数．
（2）从参加测试的“合格生”中，根据表中分组情况，按分层抽样的方法抽取8名男生，再从这8名男生中抽取3名男生，记X表示3人中“优良生”的人数，求X的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】数列{an}满足Sn＝2n－an(n∈N*)．
(1)计算a1，a2，a3，a4，并由此猜想通项公式an；
(2)用数学归纳法证明(1)中的猜想．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
过两点
， 
，且圆心
在直线
上．
（Ⅰ）求圆
的标准方程；
（Ⅱ）直线
过点
且与圆
有两个不同的交点
， 
，若直线
的斜率
大于0，求
的取值范围；
（Ⅲ）在（Ⅱ）的条件下，是否存在直线
使得弦
的垂直平分线过点
，若存在，求出直线
的方程；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知正项数列
的前n项和
满足
（1）求数列的通项公式；
（2）若
（n∈N*），求数列
的前n项和
;
（3）是否存在实数
使得
对
恒成立，若存在，求实数的取值范围，若不存在说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C：
（a＞b＞0）的两个焦点分别为F1，F2，离心率为
，过F1的直线l与椭圆C交于M，N两点，且△MNF2的周长为8．
（1）求椭圆C的方程；
（2）若直线y＝kx＋b与椭圆C分别交于A，B两点，且OA⊥OB，试问点O到直线AB的距离是否为定值，证明你的结论．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}，{bn}满足：a1＝3，当n≥2时，an﹣1+an＝4n；对于任意的正整数n，
．设{bn}的前n项和为Sn．
（1）求数列{an}及{bn}的通项公式；
（2）求满足13＜Sn＜14的n的集合．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
