
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �ٿ����p������ķ�Ҫ��Ѵ���һ����Ϊ�������x�����ѽ��۷��ʢ���ȷ������������ֵ�ķ����жϼ��ɣ�
�����������Ķ�����жϣ������ݺ����Ķ���ɵó�m=2���������⣮
��� �⣺�ٷ�p������ķ�Ҫ��Ѵ���һ����Ϊ�������x�����ѽ��۷��ʢ���ȷ��
���ɶԳƵ�����֪lga+lgb=lgab����a=2��b=2ʱ��lg��a+b��=lgab=lg4���ʢڴ���
��ԭ�����������⼴�ȷ����棬�ʢ���ȷ��
�ܵ�m=2ʱ��f��x��=x-1�������⣬�ʢ���ȷ��
��ѡ��C��
���� ��������������Ķ���Ͷ��������ʣ�ѧ��ѡ����������ֵ���������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
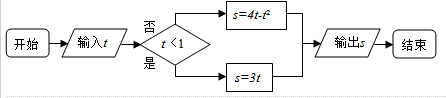
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��Ч | �Ǹ�Ч | ͳ�� | |
| �¿γ�ģʽ | 60 | 30 | 90 |
| ��ͳ����ģʽ | 40 | 50 | 90 |
| ͳ�� | 100 | 80 | 180 |
| P��K2�RK0�� | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 50 | B�� | 77 | C�� | 78 | D�� | 306 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | g��x��=sin��2x+$\frac{5��}{12}$�� | B�� | g��x��=sin��2x+$\frac{��}{12}$�� | C�� | g��x��=sin��2x-$\frac{��}{12}$�� | D�� | g��x��=sin��2x-$\frac{5��}{12}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1.2�� | B�� | ��-2��1�� | C�� | ��1��-2�� | D�� | ��2��-1�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com