
【题目】已知圆![]() ,圆
,圆![]()
(1)若圆![]() 、
、![]() 相交,求
相交,求![]() 的取值范围;
的取值范围;
(2)若圆![]() 与直线
与直线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的值;
的值;
(3)已知点![]() ,圆
,圆![]() 上一点
上一点![]() ,圆
,圆![]() 上一点
上一点![]() ,求
,求![]() 的最小值的取值范围.
的最小值的取值范围.
【答案】(1)![]() 或
或![]() ; (2)
; (2)![]() 或
或![]() ; (3)
; (3)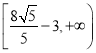 .
.
【解析】
(1)由圆![]() 、
、![]() 相交,则
相交,则![]() ,即可求解
,即可求解![]() 的取值范围;
的取值范围;
(2)由![]() 到直线
到直线![]() 的距离为
的距离为![]() ,利用弦心距,半弦长,半径构成的直角三角形,即可求解
,利用弦心距,半弦长,半径构成的直角三角形,即可求解![]() 的值;
的值;
(3)通过作圆![]() 的对称圆
的对称圆![]() ,找到
,找到![]() 的对称点
的对称点![]() ,然后将
,然后将![]() 转化为
转化为![]() ,转化为圆
,转化为圆![]() 与圆
与圆![]() 上两个动点之间距离,最后通过圆心距与两圆半径解决即可.
上两个动点之间距离,最后通过圆心距与两圆半径解决即可.
解:(1)已知圆![]() ,圆
,圆![]() ,
,
圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() ,
,
圆![]() 的圆心
的圆心![]() ,半径为
,半径为![]() ,
,
因为圆![]() 、
、![]() 相交,所以圆心距
相交,所以圆心距![]() ,
,
即![]() ,
,
解得:![]() 或
或![]() .
.
(2)因为圆![]() 与直线
与直线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,
,
而圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
结合![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() .
.
(3)已知点![]() ,圆
,圆![]() 上一点
上一点![]() ,圆
,圆![]() 上一点
上一点![]() ,
,
由向量加减运算得![]() ,
,
由![]() 联想到作出圆
联想到作出圆![]() 关于定点
关于定点![]() 的对称圆
的对称圆![]() ,
,
延长![]() 与圆
与圆![]() 交于点
交于点![]() ,则
,则![]() ,
,
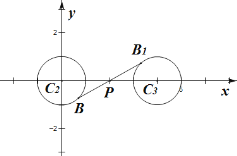
所以![]() ,
,
即![]() 就是圆
就是圆![]() 上任一点A与圆
上任一点A与圆![]() 上任一点
上任一点![]() 的距离,
的距离,
所以![]()
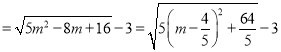
即当![]() 时,
时,![]() ,
,
所以![]() 的最小值的取值范围是
的最小值的取值范围是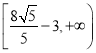 .
.


科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取![]() 人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校高一年级开设![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选![]() 课程,不选
课程,不选![]() 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中![]() 课程且乙同学未选中
课程且乙同学未选中![]() 课程的概率.
课程的概率.
(Ⅱ)用![]() 表示甲、乙、丙选中
表示甲、乙、丙选中![]() 课程的人数之和,求
课程的人数之和,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
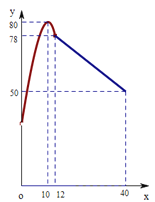
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数![]() 与听课时间
与听课时间![]() (单位:分钟)之间的关系满足如图所示的图象,当
(单位:分钟)之间的关系满足如图所示的图象,当![]() 时,图象是二次函数图象的一部分,其中顶点
时,图象是二次函数图象的一部分,其中顶点![]() ,过点
,过点![]() ;当
;当![]() 时,图象是线段
时,图象是线段![]() ,其中
,其中![]() .根据专家研究,当注意力指数大于62时,学习效果最佳.
.根据专家研究,当注意力指数大于62时,学习效果最佳.
(Ⅰ)试求![]() 的函数关系式;
的函数关系式;
(Ⅱ)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有限集![]() . 如果
. 如果![]() 中元素
中元素![]() 满足
满足![]() ,就称
,就称![]() 为“复活集”,给出下列结论:
为“复活集”,给出下列结论:
①集合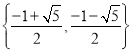 是“复活集”;
是“复活集”;
②若![]() ,且
,且![]() 是“复活集”,则
是“复活集”,则![]() ;
;
③若![]() ,则
,则![]() 不可能是“复活集”;
不可能是“复活集”;
④若![]() ,则“复活集”
,则“复活集”![]() 有且只有一个,且
有且只有一个,且![]() .
.
其中正确的结论是____________.(填上你认为所有正确的结论序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com