
【题目】学校高一年级开设![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三课程,其中甲同学必选![]() 课程,不选
课程,不选![]() 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中![]() 课程且乙同学未选中
课程且乙同学未选中![]() 课程的概率.
课程的概率.
(Ⅱ)用![]() 表示甲、乙、丙选中
表示甲、乙、丙选中![]() 课程的人数之和,求
课程的人数之和,求![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】设函数f(x)=a2x2(a>0),g(x)=bln x.
(1)若函数y=f(x)图象上的点到直线x-y-3=0距离的最小值为2![]() ,求a的值;
,求a的值;
(2)对于函数f(x)与g(x)定义域上的任意实数x,若存在常数k,m,使得f(x)≥kx+m和g(x)≤kx+m都成立,则称直线y=kx+m为函数f(x)与g(x)的“分界线”.设a=![]() ,b=e,试探究f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
,b=e,试探究f(x)与g(x)是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1, ![]() ,
, ![]() ,过动点A作
,过动点A作![]() ,垂足D在线段BC上且异于点B,连接AB,沿
,垂足D在线段BC上且异于点B,连接AB,沿![]() 将△
将△![]() 折起,使
折起,使![]() (如图2所示).
(如图2所示).

(1)当![]() 的长为多少时,三棱锥
的长为多少时,三棱锥![]() 的体积最大;
的体积最大;
(2)当三棱锥![]() 的体积最大时,设点
的体积最大时,设点![]() ,
, ![]() 分别为棱
分别为棱![]() ,
, ![]() 的中点,试在棱
的中点,试在棱![]() 上确定一点
上确定一点![]() ,使得
,使得![]()
![]() ,并求
,并求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在极坐标系中,已直曲线![]() ,将曲线C上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C1,又已知直线
,将曲线C上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C1,又已知直线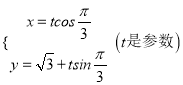 ,且直线
,且直线![]() 与C1交于A、B两点,
与C1交于A、B两点,
(1)求曲线C1的直角坐标方程,并说明它是什么曲线;
(2)设定点![]() , 求
, 求![]() 的值;
的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com