Question

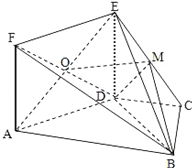
【题目】如图，边长为的正方形与梯形所在的平面互相垂直，其中, 为的中点．

（Ⅰ）证明： 平面；

（Ⅱ）求与平面所成角的余弦值．

Answer 1

【答案】（1）见解析（2）

【解析】试题分析：（Ⅰ）推导出OM∥AC，由此根据线面平行的判定定理能证明OM||平面ABCD．（Ⅱ）推导出BD⊥DA，因为平面ADEF⊥平面ABCD，从而可得BD⊥平面ADEF，由此得到∠BFD的余弦值即为所求．

试题解析：

证明：（Ⅰ）∵O，M分别为EA，EC的中点， ∴OM∥AC．

∵OM平面ABCD，AC平面ABCD…．∴OM∥平面ABCD

解：（Ⅱ） ∵DC=BC=1，∠BCD=90°，

∴∵． ∴BD⊥DA．

∵平面ADEF⊥平面ABCD，平面ADEF∩平面ABCD=AD，BD平面ABCD，

∴BD⊥平面ADEF

∴∠BFD的余弦值即为所求.

在，

∴…．

∴．