Question

已知圆，设点B,C是直线上的两点，它们的横坐标分别是，点P在线段BC上，过P点作圆M的切线PA，切点为A

（1）若，求直线的方程；

（2）经过三点的圆的圆心是，求线段(为坐标原点）长的最小值

 

Answer 1

（1）或（2）

【解析】

试题分析：（1）因为点P在线段BC上，所以可假设点P的坐标 又根据，所以可求出点P的坐标，同时要检验一下使得点P符合在线段BC上 再通过假设直线的斜率利用点到直线的距离等于圆的半径即可求出直线的斜率，从而得到切线方程

（2）因为经过三点的圆的圆心是，求线段(为坐标原点）长 通过假设点P的坐标即可表示线段PM的中点D的坐标（因为） 根据两点间的距离公式写出的表达式 接着关键是根据的范围讨论 因为的值受的大小决定的 要分三种情况讨论即i) ;ii) ,iii) 分别求出三种情况的最小值即为所求的结论

试题解析：（1）设因为，，所以 解得或（舍去） 所以 由题意知切线的斜率存在，设斜率为k 所以直线的直线方程为即

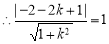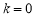直线PA与圆M相切，，解得或

直线PA的方程是或 6分

（2）设

与圆M相切于点A，

经过三点的圆的圆心D是线段MP的中点

的坐标是

设

当，即时，

当，即时，

当，即时

则

考点：1 直线与圆的位置关系知识 2求圆的切线方程的知识 3 求直角三角形的外接圆的方程的方法 4 解决动区间的二次函数的最值问题的能力 5 分类的思想方法