
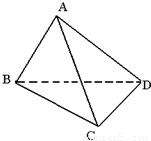
若△ABC与△DBC是有公共底边BC的两个等腰三角形,二面角A-BC-D为60°,BC=16,AB=AC=17,∠BDC=90°,则
(1)A点到BC边的距离是________;
(2)A、D两点间的距离是________;
(3)A点到平面BCD的距离是________;
(4)AD与BC间的距离是_________.
解:取BC中点E(如图甲所示)
∵ CD=BD,∴ DE⊥BC 同理AE⊥BC,又∠BDC=90°∴ ED=EC=EB=8 (1)AE ∴ A点到BC边距离是15(长度单位). (2)AD2=AE2+ED2-2·AE·ED·cos60° =152+82-2×15×8× 即AD=13 ∴ A、D两点间距离是13(长度单位) (3)∵ BC⊥平面AED ,∴ 平面AED⊥平面BCD 作AF⊥ED于F(如图乙所示) ∴ AF⊥平面BCD ∵ ∴ AF=AE·sin∠AED=15× (4)作EG⊥AD于G 又∵ BC⊥平面AED ∴ BC⊥EG,∴ EG是AD与BC的距离 ∵ ∴ EG= |


科目:高中数学 来源: 题型:
 在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
如图,四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:022
(1)A点到BC边的距离是________;
(2)A、D两点间的距离是________;
(3)A点到平面BCD的距离是________;
(4)AD与BC间的距离是_________.
查看答案和解析>>
科目:高中数学 来源:2006-2007学年北京市崇文区高三(上)期末数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com