
(本题满分12分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般 情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当
桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20
辆/千米时,车流速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度 x的一次函数.
(1)当0≤x≤200时,求函数v (x)的表达式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时)
(1)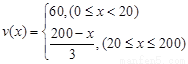 ;
;
(2)当x=100时,f(x)在区间[0,200]上取得最大值 ≈3333.
≈3333.
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
【解析】本题主要考查一次函数的应用、最值等基础知识,同时考查运用数学知识解决实际问题的能力,属于中等题.
(1)根据题意,函数v(x)表达式为分段函数的形式,关键在于求函数v(x)在20≤x≤200时的表达式,根据一次函数表达式的形式,用待定系数法可求得;
(2)先在0≤x≤20上,车流量函数为增函数,得最大值为v(20)=1200,然后在20≤x≤200上,车流量函数为二次函数,然后根据二次函数的最大值问题解答。
解:(1)由题意:当0≤x≤20时,v(x)=60;当20≤x≤200时,设v(x)=ax+b.
再由已知得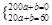 解得
解得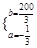 ………………………………4分
………………………………4分
故函数v(x)的表达式为
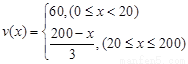 ……………………………………………………6分
……………………………………………………6分
(2)依题意并由(1)可得
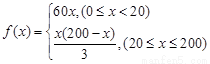 ………………………………………8分
………………………………………8分
当0≤x≤20时,f(x)为增函数,故当x=20时,其最大值为60×20=1200;……9分
当20≤x≤200时,f(x)=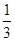 x(200-x)≤
x(200-x)≤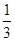
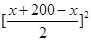 =
= . ……………10分
. ……………10分
当且仅当x=200-x,即x=100时,等号成立.
所以,当x=100时,f(x)在区间[20,200]上取得最大值 .……………11分
.……………11分
综上,当x=100时,f(x)在区间[0,200]上取得最大值 ≈3333.
≈3333.
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
………12分


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:正定中学2010高三下学期第一次考试(数学文) 题型:解答题
(本题满分12分)
直线 过点P
过点P (
( 斜率为
斜率为 ,与直线
,与直线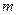 :
: 交于点A,与
交于点A,与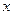 轴交于点B,点A,B的横坐标分别为
轴交于点B,点A,B的横坐标分别为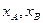 ,记
,记 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)设数列 满足
满足 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,当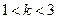 时,证明不等式
时,证明不等式 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省卢氏一高高三适应性考试理科数学 题型:解答题
(本小题满分12分) 提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数
(1)当0≤x≤200时,求函数v(x)的表达式
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省沈阳四校协作体高二上学期期中考试数学 题型:解答题
((本题满分12分)提高过浑河大桥的车辆通行能力可改善整个沈城的交通状况.在一般情况下,浑河大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数记作 .当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当
.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.
(1)当 时,求函数
时,求函数 的表达式;
的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
查看答案和解析>>
科目:高中数学 来源:2010年哈尔滨市高二下学期期末考试文科数学卷 题型:解答题
(本题满分12分)
设过点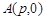
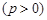 的直线
的直线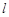 交抛物线
交抛物线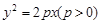 于B、C两点,
于B、C两点,
(1)设直线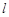 的倾斜角为
的倾斜角为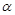 ,写出直线
,写出直线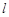 的参数方程;
的参数方程;
(2)设P是BC的中点,当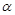 变化时,求P点轨迹的参数方程,并化为普通方程.
变化时,求P点轨迹的参数方程,并化为普通方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com