
【题目】“工资条里显红利,个税新政人民心”,随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段,某![]() 从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁~35岁(2009年~2018年)之间各月的月平均收入
从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁~35岁(2009年~2018年)之间各月的月平均收入![]() (单位:千元)的散点图:
(单位:千元)的散点图:
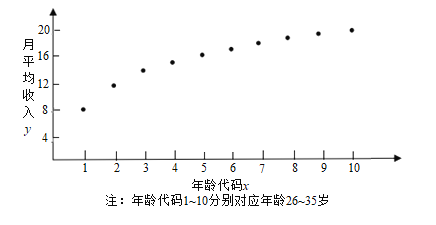
(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据有关数据建立
的关系,试根据有关数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)如果该![]() 从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入为月收入,根据新旧个税政策,估计他36岁时每个月少缴交的个人所得税.
从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入为月收入,根据新旧个税政策,估计他36岁时每个月少缴交的个人所得税.
附注:
参考数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ;取
;取![]() ,
,![]()
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为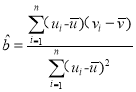 ,
,![]()
新旧个税政策下每月应纳税所得额(含税)计算方法及税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
税缴级数 | 每月应纳税所得额(含税) =收入-个税起征点 | 税率 (%) | 每月应纳税所得额(含税) =收入一个税起征点-专项附加扣除 | 税率 (%) |
1 | 不超过1500元的部分 | 3 | 不超过3000元的部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元155000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
【答案】(1)![]() ;(2)2130元.
;(2)2130元.
【解析】
(1)由题意,令![]() ,根据最小二乘法的计算公式,分别求得
,根据最小二乘法的计算公式,分别求得![]() 的值,即可得到回归直线的方程;
的值,即可得到回归直线的方程;
(2)由(1)得该IT从业人员36岁时月平均收入,再利用表格中的数据和个税的计算方法,求得新旧个税政策下缴交的个人所得税,即可得到答案.
(1)由题意,令![]() ,则
,则![]()
由最小二乘法的公式,可得 ,
,
又由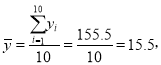
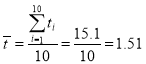 ,
,
所以![]() ,
,
所以![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ,
,
因为![]() ,从而
,从而![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
(2)由(1)得该IT从业人员36岁时月平均收入为:![]() (千元),
(千元),
旧个税政策下缴交的个人所得税为:
![]() (元),
(元),
新个税政策下缴交的个人所得税为:
![]() (元),
(元),
故根据新旧个税政策,
则该IT从业人员36岁时每个月少缴交的个人所得税为![]() (元).
(元).


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】某中学有学生500人,学校为了解学生的课外阅读时间,从中随机抽取了50名学生,获得了他们某一个月课外阅读时间的数据(单位:小时),将数据分为5组:[10,12),[12,14),[14,16),[16,18),[18,20],整理得到如图所示的频率分布直方图.
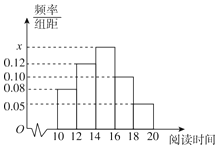
(1)求频率分布直方图中的x的值;
(2)试估计该校所有学生中,课外阅读时间不小于16小时的学生人数;
(3)已知课外阅读时间在[10,12)的样本学生中有3名女生,现从阅读时间在[10,12)的样本学生中随机抽取3人,记X为抽到女生的人数,求X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a,b
(a,b![]() R).
R).
(1)当a=b=1时,求![]() 的单调增区间;
的单调增区间;
(2)当a≠0时,若函数![]() 恰有两个不同的零点,求
恰有两个不同的零点,求![]() 的值;
的值;
(3)当a=0时,若![]() 的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
的解集为(m,n),且(m,n)中有且仅有一个整数,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC—A1B1C1中,四边形AA1B1B为矩形,平面AA1B1B⊥平面ABC,点E,F分别是侧面AA1B1B,BB1C1C对角线的交点.
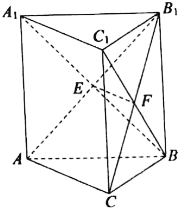
(1)求证:EF∥平面ABC;
(2)BB1⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(2)是否存在实数![]() ,
,![]() 同时满足下列条件:①
同时满足下列条件:①![]() ;②当
;②当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() ,
,![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]() 在区间
在区间![]() ,
,![]() 内各有一个极值点.
内各有一个极值点.
(I)求![]() 的最大值;
的最大值;
(II)当![]() 时,设函数
时,设函数![]() 在点
在点![]() 处的切线为
处的切线为![]() ,若
,若![]() 在点
在点![]() 处穿过函数
处穿过函数![]() 的图象(即动点在点
的图象(即动点在点![]() 附近沿曲线
附近沿曲线![]() 运动,经过点
运动,经过点![]() 时,从
时,从![]() 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把![]() ,
,![]() ,
,![]() ,
,![]() 四本不同的书分给三位同学,每人至少分到一本,每本书都必须有人分到,
四本不同的书分给三位同学,每人至少分到一本,每本书都必须有人分到,![]() ,
,![]() 不能同时分给同一个人,则不同的分配方式共有__________种(用数字作答).
不能同时分给同一个人,则不同的分配方式共有__________种(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某种细菌的繁殖个数y随天数x的变化情况,收集数据如下:
天数x | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数y | 6 | 12 | 25 | 49 | 95 | 190 |
(1)根据散点图,判断![]() 与
与![]() 哪一个适合作为y关于x的回归方程类型;(给出判断即可,不用说明理由)
哪一个适合作为y关于x的回归方程类型;(给出判断即可,不用说明理由)
(2)根据(1)中的判断及表中数据,求y关于x的回归方程![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
参考公式: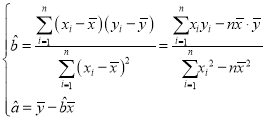
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com