【题目】斜率为2的直线l在双曲线
上截得的弦长为
，求l的方程．
【答案】y＝2x±
【解析】
设直线
的方程为
,设和双曲线的两交点为
，将直线方程代入双曲线方程可得到关于
的一元二次方程，根据韦达定理可用
表示
,然后求弦长等于
,这样可得到关于的方程，解方程即得的值，从而便求出来直线的方程.
设直线l的方程为y＝2x＋m，
由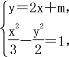
得10x2＋12mx＋3(m2＋2)＝0.(*)
设直线l与双曲线交于A(x1，y1)，B(x2，y2)两点，由根与系数的关系，
得x1＋x2＝－
m，x1x2＝
(m2＋2)．
∴|AB|2＝(x1－x2)2＋(y1－y2)2＝5(x1－x2)2＝5[(x1＋x2)2－4x1x2]＝5
.∵|AB|＝
，∴
m2－6(m2＋2)＝6，∴m2＝15，m＝±
.
由(*)式得Δ＝24m2－240，
把m＝±代入上式，得Δ>0，∴m的值为±，
∴所求l的方程为y＝2x±.
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c且满足csinA=acosC，
（1）求角C的大小；
（2）求 
sinA﹣cos（B+ 
）的最大值，并求取得最大值时角A，B的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知一个口袋内有4个不同的红球,6个不同的白球.
(1)从中任取4个球,红球的个数不比白球的个数少的取法有多少种?
(2)从中任取5个球,记取到红球的个数为X,求X的分布列和数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数f（x）=axn（1﹣x）（x＞0，n∈N*），当n=﹣2时，f（x）的极大值为 
．
（1）求a的值；
（2）求证：f（x）+lnx≤0；
（3）求证：f（x）＜ 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线y2=8x的准线与双曲线 
﹣ 
=1（a＞0，b＞0）相交于A、B两点，双曲线的一条渐近线方程是y= 
x，点F是抛物线的焦点，且△FAB是等边三角形，则该双曲线的标准方程是（ ）
A.
﹣ 
=1
B.
﹣ 
=1
C.
﹣ 
=1
D.
﹣ 
=1
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．
（1）证明：PB∥平面AEC；
（2）已知AP=AB=1，AD= 
，求二面角D﹣AE﹣C的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题p:函数f(x)=|2x+3c|在[-1,+∞)上单调递增;命题q:函数g(x)=
+2有零点.
(1)若命题p和q均为真命题,求实数c的取值范围;
(2)是否存在实数c,使得p∧(q)是真命题?若存在,求出c的取值范围;若不存在,说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知动点M（x，y）到直线ι：x=4的距离是它到点N（1，0）的距离的2倍．
（1）求动点M的轨迹C的方程；
（2）过点P（0，3）的直线m与轨迹C交于A，B两点，若A是PB的中点，求点A的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
