Question

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．

（1）证明：PB∥平面AEC；
（2）已知AP=AB=1，AD= ，求二面角D﹣AE﹣C的余弦值．

Answer 1

【答案】
（1）证明：连结AC、BD，交于点O，连结OE，

∵底面ABCD为矩形，∴O是BD中点，

∵E为PD的中点，∴OE∥PB，

∵PB平面AEC，OE平面AEC，

∴PB∥平面AEC．

（2）解：以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，

∵AP=AB=1，AD= ，

∴A（0，0，0），C（1， ，0），P（0，0，1），D（0， ，0），E（0， ， ），

=（1， ，0）， =（0， ， ），

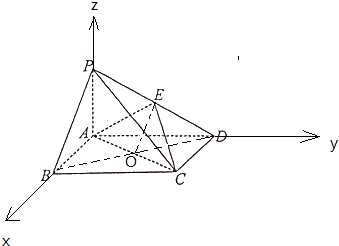
设平面AEC的法向量 =（x，y，z），

则 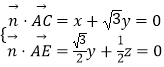，取x=3，得 =（3，﹣ ，3），

又平面DEA的法向理 =（1，0，0），

设二面角D﹣AE﹣C的平面角为θ，

则cosθ= = = ．

∴二面角D﹣AE﹣C的余弦值为 ．

【解析】（1）连结AC、BD，交于点O，连结OE，则OE∥PB，由此能证明PB∥平面AEC．（2）以A为原点，AB为x轴，AD为y轴，AP为z轴，建立空间直角坐标系，利用向量法能求出二面角D﹣AE﹣C的余弦值．
【考点精析】关于本题考查的直线与平面平行的判定，需要了解平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能得出正确答案．