

(1)△AOB面积的最小值及此时直线l的方程;
(2)求直线l在两坐标轴上截距之和的最小值及此时直线l的方程;
(3)求|PA|·|PB|的最小值及此时直线l的方程.
思路解析:本题的关键是何时取得最值.可以先设出斜率,分别求出|OA|,|OB|,然后再由不等式、判别式或三角变换等有关方法来求.
(1)解法一:设直线l的方程为y-1=k(x-2).
令y=0,得x=![]() ;令x=0,得y=1-2k.
;令x=0,得y=1-2k.
∴A、B两点坐标分别为A(![]() ,0),B(0,1-2k).
,0),B(0,1-2k).
∵A、B是l与x轴、y轴正半轴的交点,
∴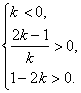
S△ABC=![]() ·|OA|·OB|=
·|OA|·OB|=![]() ·
·![]() ·(1-2k)=
·(1-2k)=![]() (4-
(4-![]() -4k).
-4k).
由-![]() >0,-4k>0,有-
>0,-4k>0,有-![]() -4k≥2
-4k≥2![]() =4.
=4.
当且仅当-![]() =-4k,即k=-
=-4k,即k=-![]() 时,-
时,-![]() -4k取最小值4.
-4k取最小值4.
∴S△AOB的最小值为![]() ×(4+4)=4.
×(4+4)=4.
此时l的方程是y-1=-![]() (x-2),即x+2y-4=0.
(x-2),即x+2y-4=0.
解法二:设l的方程为![]() +
+![]() =1(a>0,b>0).
=1(a>0,b>0).
∵点P(2,1)在l上,∴![]() +
+![]() =1.
=1.
又∵![]() +
+![]() ≥2
≥2![]() ,∴2
,∴2![]() ≤1.
≤1.
∴![]() ab≥4.
ab≥4.
当且仅当![]() =
=![]() =
=![]() ,即a=4,b=2时,△AOB面积S=
,即a=4,b=2时,△AOB面积S=![]() ab有最小值4.
ab有最小值4.
此时直线l的方程为![]() +
+![]() =1.
=1.
解法三:由解法一知S=![]() ·
·![]() ·(1-2k),
·(1-2k),
整理得4k2+2(S-2)k+1=0.
∵k∈R,∴Δ=4(S-2)2-4×4×1≥0.解得S≥4.
当且仅当S=4时,k=-![]() .
.
∴△AOB面积的最小值为4.
当△AOB面积最小时,l的方程为y-1=-![]() (x-2),即x+2y-4=0.
(x-2),即x+2y-4=0.
解法四:由解法二可知![]() +
+![]() =1,∴b=
=1,∴b=![]() . ①
. ①
△AOB的面积S=![]() ·a·b=
·a·b=![]() ·a·
·a·![]() =
=![]() , ②
, ②
整理得a2-2aS+4S=0.
∵a∈R,∴Δ=4S2-4×4S≥0,(S>0).∴S≥4.
将S=4代入②,得a=4;将a=4代入①,得b=2.
∴△AOB面积的最小值为4.
此时直线l的方程为![]() +
+![]() =1,即x+2y-4=0.
=1,即x+2y-4=0.
(2)解法一:∵A(![]() ,0),B(0,1-2k)(k<0=,
,0),B(0,1-2k)(k<0=,
∴截距之和为![]() +1-2k=3-2k-
+1-2k=3-2k-![]() =3+(-2k)+(-
=3+(-2k)+(-![]() )≥3+2
)≥3+2![]() =3+2
=3+2![]() .
.
此时-2k=-![]() ,即k=-
,即k=-![]() .故截距之和的最小值为3+2
.故截距之和的最小值为3+2![]() .
.
此时l的方程为y-1=-![]() (x-2).
(x-2).
解法二:∵![]() +
+![]() =1(a>0,b>0),
=1(a>0,b>0),
∴a+b=(a+b)(![]() +
+![]() )=2+1+
)=2+1+![]() +
+![]() =3+
=3+![]() +
+![]() ≥3+2
≥3+2![]() =3+2
=3+2![]() .
.
此时![]() =
=![]() ,即2b2=a2.求得b=
,即2b2=a2.求得b=![]() +1,a=2+
+1,a=2+![]() .
.
故截距之和的最小值为3+2![]() .
.
∴此时直线l的方程为![]() +
+![]() =1,即y-1=-
=1,即y-1=-![]() (x-2).
(x-2).
轻轻告诉你 行不义的人比遭受这个不义行为的人更不幸。——德谟克利特
(3)解法一:∵A(2-![]() ,0),B(0,1-2k)(k<0),
,0),B(0,1-2k)(k<0),
∴|PA|·|PB|=![]() ·
·![]() =2[
=2[![]() +(-k)]≥4.
+(-k)]≥4.
当且仅当-k=-![]() ,即k=-1时上式等号成立.
,即k=-1时上式等号成立.
故|PA|·|PB|的最小值为4.此时直线l的方程为x+y-3=0.
解法二:∵|PA|=![]() ,|PB|=
,|PB|=![]() ,
,
∴|PA|·|PB|=![]() =
=![]() .
.
当θ=45°时,直线l的斜率为-1,此时|PA|·|PB|有最小值4,直线l的方程为x+y-3=0.
深化升华
以上三个小题的各种方法概括起来就是利用直线的斜率、截距及角θ作为参变量,利用均值不等式或判别式法求最值.一般来说,总是把所求的问题,如面积、截距之和、距离之积归结为关于斜率k、角θ或截距的表达式,再去解决问题.这也是解析几何中常用的代数手段.尤其是利用不等式求最值,今后会常遇到.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
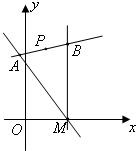 如图,过点P(1,5)作直线l,与直线a:y=-
如图,过点P(1,5)作直线l,与直线a:y=-| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
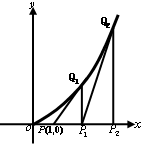 (2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.
(2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.| 1 |
| d1 |
| 1 |
| d2 |
| 1 |
| dn |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省韶关市高三4月第二次调研测试数学理科试卷(解析版) 题型:解答题
如图,过点P(1,0)作曲线C: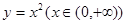 的切线,切点为
的切线,切点为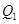 ,设点
,设点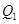 在
在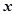 轴上的投影是点
轴上的投影是点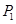 ;又过点
;又过点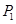 作曲线
作曲线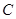 的切线,切点为
的切线,切点为 ,设
,设 在
在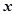 轴上的投影是
轴上的投影是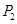 ;………;依此下去,得到一系列点
;………;依此下去,得到一系列点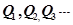
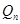 ,设点
,设点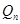 的横坐标为
的横坐标为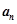 .
.
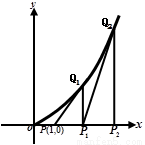
(1)求直线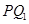 的方程;
的方程;
(2)求数列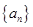 的通项公式;
的通项公式;
(3)记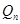 到直线
到直线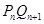 的距离为
的距离为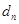 ,求证:
,求证: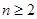 时,
时,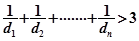
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
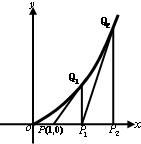 如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.
如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.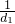 +
+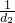 +…
+…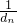 >3.
>3.查看答案和解析>>
科目:高中数学 来源:2013年广东省韶关市高考数学二模试卷(理科)(解析版) 题型:解答题
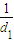 +
+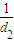 +…
+…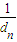 >3.
>3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com