
【题目】在平面直角坐标系xOy中,椭圆C的参数方程为 ![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为 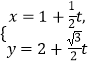 (t为参数).
(t为参数).
(Ⅰ)写出椭圆C的普通方程和直线l的倾斜角;
(Ⅱ)若点P(1,2),设直线l与椭圆C相交于A,B两点,求|PA|·|PB|的值.
【答案】解:(Ⅰ)消去θ得到椭圆C的普通方程为 ![]() .
.
∵直线 ![]() 的斜率为
的斜率为 ![]() ,∴直线l的倾斜角为
,∴直线l的倾斜角为 ![]() .
.
(Ⅱ)把直线 ![]() 的方程
的方程 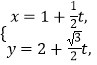 ,代入
,代入 ![]() 中,
中,
得 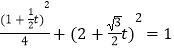 .
.
即 ![]() ,
,
∴t1·t2=4,即|PA|·|PB|=4.
【解析】(Ⅰ)利用sin2θ+cos2θ=1消去θ,从而得到椭圆的普通方程,根据参数方程可知直线l定过点(1,2),从而斜率为![]() ,即为
,即为![]() ,从而求得直线l的倾斜角;(Ⅱ)因为
,从而求得直线l的倾斜角;(Ⅱ)因为![]() ,所以|PA|·|PB|=t1·t2=4.
,所以|PA|·|PB|=t1·t2=4.
【考点精析】根据题目的已知条件,利用直线的倾斜角和椭圆的标准方程的相关知识可以得到问题的答案,需要掌握当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α=0°;椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,满足a1=1,ak+1﹣ak=ai . (i≤k,k=1,2,3,…,n﹣1)
(1)求证: ![]() ;
;
(2)若{an}是等比数列,求数列{an}的通项公式;
(3)设数列{an}的前n项和为Sn , 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准如下:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知某学校学生的原始成绩均分布在[50,100]内,为了了解该校学生的成绩,抽取了50名学生的原始成绩作为样本进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出样本频率分布直方图如图所示.
(Ⅰ)求图中x的值,并根据样本数据估计该校学生学业水平测试的合格率;
(Ⅱ)在选取的样本中,从70分以下的学生中随机抽取3名学生进行调研,用X表示所抽取的3名学生中成绩为D等级的人数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是公差不为零的等差数列,满足
是公差不为零的等差数列,满足![]() 数列
数列![]() 的通项公式为
的通项公式为![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)将数列![]() ,
,![]() 中的公共项按从小到大的顺序构成数列
中的公共项按从小到大的顺序构成数列![]() ,请直接写出数列
,请直接写出数列![]() 的通项公式;
的通项公式;
(3)记![]() ,是否存在正整数
,是否存在正整数![]()
![]() ,使得
,使得![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图、正视图、侧视图、俯视图如图,M,N分别为A1B,B1C1的中点.
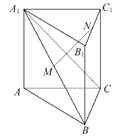
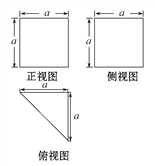
下列结论中正确的个数有 ( )
①直线MN与A1C相交.
②MN⊥BC.
③MN∥平面ACC1A1.
④三棱锥N-A1BC的体积为![]() =
=![]() a3.
a3.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:![]() 与
与![]() 轴相切.
轴相切.
(1)求![]() 的值;
的值;
(2)求圆M在![]() 轴上截得的弦长;
轴上截得的弦长;
(3)若点![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作直线
作直线![]() 与圆M相切,
与圆M相切,![]() 为切点,求四边形
为切点,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)先将圆的一般方程化成标准方程,利用直线和圆相切进行求解;(2) 令![]() ,得到关于
,得到关于![]() 的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
的一元二次方程进行求解;(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.
试题解析:(1) ![]() ∵圆M:
∵圆M:![]() 与
与![]() 轴相切
轴相切
∴![]() ∴
∴![]()
(2) 令![]() ,则
,则![]() ∴
∴![]()
∴![]()
(3) ![]()
∵![]() 的最小值等于点
的最小值等于点![]() 到直线
到直线![]() 的距离,
的距离,
∴![]() ∴
∴![]()
∴四边形![]() 面积的最小值为
面积的最小值为![]() .
.
【题型】解答题
【结束】
20
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的方程为
的方程为![]() ,且圆
,且圆![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,设直线
两点,设直线![]() 的方程为
的方程为![]() .
.
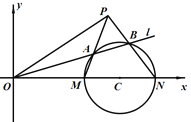
(1)当直线![]() 与圆
与圆![]() 相切时,求直线
相切时,求直线![]() 的方程;
的方程;
(2)已知直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
, ![]() 两点.
两点.
(ⅰ)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(ⅱ)直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,
, ![]() ,
,
是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com