
(14分)已知f(x)是定义在[—1,1]上的奇函数,且f (1)=1,若m,n∈[—
1,1],m+n≠0时有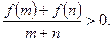
(1)判断f (x)在[—1,1]上的单调性,并证明你的结论;
(2)解不等式: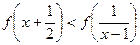 ;
;
(3)若f (x)≤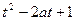 对所有x∈[—1,1],
对所有x∈[—1,1],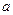 ∈[—1,1]恒成立,求实数t的取值范围.
∈[—1,1]恒成立,求实数t的取值范围.
解:(1)任取—1≤x1<x2≤1,则
f (x1)—f (x2)=" f" (x1)+f (-x2)=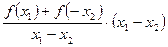
∵—1≤x1<x2≤1,∴x1+(-x2)≠0,
由已知 >0,又x1-x2<0,
>0,又x1-x2<0,
∴f (x1)—f (x2)<0,即f (x)在[—1,1]上为增函数.
(2) ∵f (x)在[—1,1]上为增函数,故有
(3)由(1)可知:f(x)在[—1,1]上是增函数,且f (1)=1,故对x∈[—l,1],恒有f(x)≤1.
所以要使f(x)≤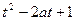 ,对所有x∈[—1,1],
,对所有x∈[—1,1],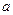 ∈[—1,1]恒成立,
∈[—1,1]恒成立,
即要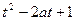 ≥1成立,故
≥1成立,故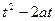 ≥0成立.
≥0成立.
记g(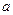 )=
)=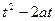 对
对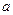 ∈[—1,1],g(
∈[—1,1],g(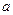 )≥0恒成立,只需g(
)≥0恒成立,只需g(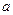 )在[—1,1]上的最小值大于等于零.
)在[—1,1]上的最小值大于等于零.
故
解得:t≤—2或t=0.
解析


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:解答题
(12分)(2010·无锡模拟)已知f(x)在定义域(0,+∞)上为增函数,且满足f(xy)=f(x)+f(y),f(3)=1,试解不等式f(x)+f(x-8)≤2.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某化工厂生产一种溶液,按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次减少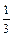 ,问过滤几次
,问过滤几次 才能使产品达到市场要求?
才能使产品达到市场要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com