请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A、B、C、D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE＝FB＝xcm.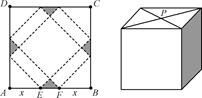
(1)某广告商要求包装盒侧面积S(cm2)最大，试问x应取何值？
(2)某厂商要求包装盒容积V(cm3)最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值．
科目：高中数学 来源： 题型：解答题
某工厂产生的废气经过过滤后排放，过滤过程中废气的污染物数量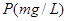
与时间
小时
间的关系为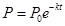
．如果在前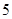
个小时消除了
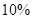的污染物，试求：
（1）
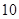个小时后还剩百分之几的污染物？
（2）污染物减少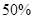
所需要的时间．（参考数据：
）
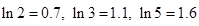查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知美国苹果公司生产某款iPhone手机的年固定成本为40万美元，每生产1万只还需另投入16万美元．设苹果公司一年内共生产该款iPhone手机x万只并全部销售完，每万只的销售收入为R(x)万美元，且R(x)＝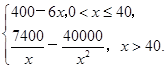
(1)写出年利润W(万美元)关于年产量x(万只)的函数解析式；
(2)当年产量为多少万只时，苹果公司在该款iPhone手机的生产中所获得的利润最大？并求出最大利润．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)＝lg(ax－bx)(a>1>b>0)．
(1)求函数y＝f(x)的定义域；
(2)在函数y＝f(x)的图象上是否存在不同的两点，使过此两点的直线平行于x轴；
(3)当a、b满足什么关系时，f(x)在区间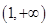
上恒取正值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某企业拟建造如图所示的容器(不计厚度，长度单位：米)，其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的容积为
立方米，且l≥2r.假设该容器的建造费用仅与其表面积有关，已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为c(c>3)千元．设该容器的建造费用为y千元．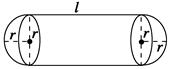
①写出y关于r的函数表达式，并求该函数的定义域；
②求该容器的建造费用最小时的r.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出场单价就降低0.02元，根据市场调查，销售商一次订购量不会超过600件．
(1)设一次订购x件，服装的实际出厂单价为p元，写出函数p＝f(x)的表达式；
(2)当销售商一次订购多少件服装时，该厂获得的利润最大？其最大利润是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
．
的值；
的不等式：
在区间
上有解，求实数
的取值范围．
＋
＝
；
.