Question

某个体经营者把开始六个月试销A、B两种商品的逐月投资与所获纯利润列成下表:

投资A种商品金额(万元)	1	2	3	4	5	6
获纯利润(万元)	0.65	1.39	1.85	2	1.84	1.40
投资B种商品金额(万元)	1	2	3	4	5	6
获纯利润(万元)	0.25	0.49	0.76	1	1.26	1.51

该经营者准备下月投入12万元经营这两种产品,但不知投入A、B两种商品各多少才最合算.请你帮助制定一个资金投入方案,使得该经营者能获得最大利润,并按你的方案求出该经营者下月可获得的最大纯利润.(结果保留两个有效数字)

Answer 1

思路分析：本题主要考查选择函数模型解决实际问题和处理数据的能力.画出散点图，调用相关函数的知识，猜测出函数模型，然后解出函数解析式来处理问题.

解：设投资额为x万元时，获得的利润为y万元.在直角坐标系中画出散点图并依次连接各点，如下图所示，

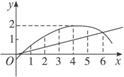
    观察散点图可知图像接近直线和抛物线，因此可考虑用二次函数描述投入A这种商品的利润y万元与投资额x万元之间的函数关系；用一次函数描述投入B这种商品的利润y万元与投资额x万元之间的函数关系.

    设二次函数的解析式为y=-a(x-4)²+2(a＞0),一次函数的解析式为y=bx.

    把x=1,y=0.65代入y=-a(x-4)²+2(a＞0)，得0.65=-a(1-4)²+2,解得a=0.15.

    故前六个月所获纯利润关于月投资A种商品的金额的函数关系可近似的用y=-0.15(x-4)²+2表示.

    把x=4,y=1代入y=bx，得b=0.25,

    故前六个月所获纯利润关于月投资B种商品的金额的函数关系可近似的用y=0.25x表示.

    令下月投入A、B两种商品的资金分别为x_a万元,x_b万元时，总利润为W万元,得

W=y_a+y_b=-0.5(x_a-4)²+2+0.25x_b，其中x_a+x_b=12.

    则W=-0.15(x_a)²+0.15·()²+2.6(0≤x_a≤12).

    则当x_a=196≈3.2万元时,W取得最大值,0.15·()²+2.6≈4.1万元,此时x_b=≈8.8万元.

    即投入A商品3.2万元，投入B商品8.8万元时，下月可获得最大纯利润4.1万元.