
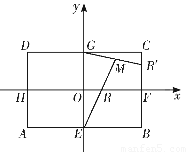
��ͼ������ABCD�У�|AB|��2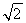 ��|BC|��2��E��F��G��H�ֱ������������ߵ��е㣬�ֱ���HF��EG������ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ����֪
��|BC|��2��E��F��G��H�ֱ������������ߵ��е㣬�ֱ���HF��EG������ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ����֪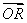 ����
����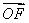 ��
��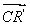 ����
����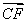 ������0������1��
������0������1��
��1����֤��ֱ��ER��GR���Ľ���M����Բ����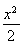 ��y2��1�ϣ�
��y2��1�ϣ�
��2������N��ֱ��l��y��x��2���Ҳ����������ϵ�����һ�㣬F1��F2�ֱ�Ϊ��Բ�������ҽ�����ֱ��NF1��NF2����Բ���Ľ���ֱ�ΪP��Q��S��T���Ƿ���ڵ�N��ʹ��ֱ��OP��OQ��OS��OT��б��kOP��kOQ��kOS��kOT����kOP��kOQ��kOS��kOT��0�������ڣ������N�����ꣻ�������ڣ���˵��������
��1����������2�����������ĵ�N������������Ϊ
��������
����������������������ò��� ��ʾ��
��ʾ�� �����꣬����ʽд��ֱ��
�����꣬����ʽд��ֱ�� �ķ��̣���������ǵĽ���
�ķ��̣���������ǵĽ��� �����꣬��ȥ�������ɵ�֤.��2��������ڵ�
�����꣬��ȥ�������ɵ�֤.��2��������ڵ�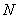 ��ֱ��
��ֱ��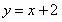 �ϣ�ʹ
�ϣ�ʹ ,
,
�� ��
�� ��
�� ,
, ��
�� ֱ��
ֱ�� ��б��Ϊ
��б��Ϊ ��ֱ��
��ֱ�� ��б��Ϊ
��б��Ϊ ����д����ֱ�ߵķ��̣����ֱ�����Բ����������ɷ��̼�������һԪ���η��̸���ϵ���Ĺ�ϵ���������
����д����ֱ�ߵķ��̣����ֱ�����Բ����������ɷ��̼�������һԪ���η��̸���ϵ���Ĺ�ϵ��������� ̽��
̽�� ��
�� �Ĺ�ϵ���Ӷ�ȷ������
�Ĺ�ϵ���Ӷ�ȷ������ �ķ��̵ĸ��Ĵ����ԣ�Ҳ���ǵ�
�ķ��̵ĸ��Ĵ����ԣ�Ҳ���ǵ� �Ĵ�����.
�Ĵ�����.
�����������1������֪����F( ��0)��C(
��0)��C( ��1)��
��1)��
�� ����
���� ��
�� ����
���� ����R(
����R( ����0)��R��(
����0)��R��( ��1����)��
��1����)��
��E(0����1)��G(0��1)����
ֱ��ER�ķ���Ϊy��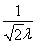 x��1�� ��
x��1�� ��
ֱ��GR��������Ϊy���� x��1�� ��
x��1�� ��
���٢ڣ���M( ��
�� )��
)��
�� ��(
��( )2��
)2�� ��
�� ��1��
��1��
��ֱ��ER��GR���Ľ���M����Բ���� ��y2��1�ϣ� 5��
��y2��1�ϣ� 5��
��2���������������ĵ�N(x0��y0)��������
ֱ��NF1�ķ���Ϊy��k1(x��1)������k1�� ��
��
ֱ��NF2�ķ���Ϊy��k2(x��1)������k2�� ��
��
����ȥy������(2k12��1)x2��4k12x��2k12��2��0��
��P(x1��y1)��Q(x2��y2)����x1��x2���� ��x1x2��
��x1x2�� ��
��
��OP��OQ��б�����ڣ���x1��0��x2��0����k12��1��
��kOP��kOQ�� ��
�� ��
�� ��
�� ��2k1��k1��
��2k1��k1�� ��k1(2��
��k1(2�� )����
)���� ��
��
ͬ���ɵ�kOS��kOT���� ��
��
��kOP��kOQ��kOS��kOT����2( ��
�� )����2��
)����2�� ����
���� ��
��
��kOP��kOQ��kOS��kOT��0������ ��0����(k1��k2)(k1k2��1)��0��
��0����(k1��k2)(k1k2��1)��0��
����N��������������֪k1��k2��0��
��k1k2��1���� ��
�� ��1�� ��
��1�� ��
��y0��x0��2�� ��
��ۢܣ���x0���� ��y0��
��y0�� ��
��
�����������ĵ�N������������Ϊ���� ��
�� ���� 13��
���� 13��
���㣺1������켣���̵���2��ֱ������Բ��λ�ù�ϵ��Ӧ�ã�3��ƽ�������������ʾ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ������ABCD�У�AB=
��ͼ������ABCD�У�AB=8
| ||
| 3 |
| 2�� |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 A ������ax-x-a=0������ʵ���⣬��a��ȡֵ��Χ��
A ������ax-x-a=0������ʵ���⣬��a��ȡֵ��Χ��| AE |
| AF |
| 9 |
| 2 |
| 9 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ������ABCD�У�DC=
��ͼ������ABCD�У�DC=| 3 |
2
| ||||
| 12 |
2
| ||||
| 12 |
| 3 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��������ͼ������ABCD�У�AB=1��BC=a��PA��ƽ��ABCD
��������ͼ������ABCD�У�AB=1��BC=a��PA��ƽ��ABCD| PQ |
| QD |
| BP |
| QD |
| ||
| 10 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com