
x+1).
(1)求f(0),f(1);
(2)求函数f(x)的解析式;
(3)若f(a-1)<-1,求实数a的取值范围.
解析: (1)因为当x≤0时,f(x)= (-x+1),
(-x+1),
所以f(0)=0.
又函数f(x)是定义在R上的偶函数,所以f(1)=f(-1)= [-(-1)+1]=
[-(-1)+1]= 2=-1,即f(1)=-1.
2=-1,即f(1)=-1.
(2)令x>0,则-x<0,
从而f(-x)= (x+1)=f(x),
(x+1)=f(x),
∴x>0时,f(x)= (x+1).
(x+1).
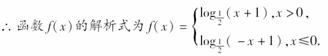
(3)设x1,x2是任意两个值,且x1<x2≤0,
则-x1>-x2≥0,
∴1-x1>1-x2>0.
∵f(x2)-f(x1)= (-x2+1)-
(-x2+1)- (-x1+1)=
(-x1+1)=
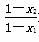 >
> 1=0,
1=0,
∴f(x2)>f(x1),
∴f(x)= (-x+1)在(-∞,0]上为增函数.
(-x+1)在(-∞,0]上为增函数.
又f(x)是定义在R上的偶函数,
∴f(x)在(0,+∞)上为减函数.
∵f(a-1)<-1=f(1),∴|a-1|>1,解得a>2或a<0.
故实数a的取值范围为(-∞,0)∪(2,+∞).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
已知直线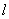 与双曲线
与双曲线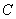 交于
交于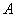 ,
,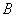 两点(
两点(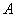 ,
,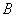 在同一支上),
在同一支上),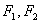 为双曲线的两个焦点,则
为双曲线的两个焦点,则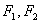 在( )
在( )
A.以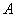 ,
,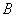 为焦点的椭圆上或线段
为焦点的椭圆上或线段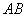 的垂直平分线上
的垂直平分线上
B.以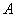 ,
,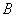 为焦点的双曲线上或线段
为焦点的双曲线上或线段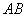 的垂直平分线上
的垂直平分线上
C.以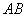 为直径的圆上或线段
为直径的圆上或线段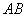 的垂直平分线上
的垂直平分线上
D.以上说法均不正确
查看答案和解析>>
科目:高中数学 来源: 题型:
若函数f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且一个零点是2,则使得f(x)<0的x的取值范围是( )
A.(-∞,-2] B.(-∞,-2)∪(2,+∞)
C.(2,+∞) D.(-2,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
若α,β是一组基底,向量γ=xα+yβ(x,y∈R),则称(x,y)为向量γ在基底α,β下的坐标,现已知向量a在基底p=(1,-1),q=(2,1)下的坐标为(-2,2),则a在另一组基底m=(-1,1),n=(1,2)下的坐标为( )
A.(2,0) B.(0,-2)
C.(-2,0) D.(0,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com