练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在等差数列{an}中，a1＞0且a5=2a10，Sn表示{an}的前n项的和，则Sn中最大的值是（ ）
    A．S14
    B．S15
    C．S13或S14
    D．S14或S15
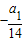
    【答案】分析：由题意可得数列的公差d=＜0，数列递减，令通项公式an≤0，解不等式可得：故数列的前14项为正，第15项为0，从第16项开始为负，进而可得答案．
    解答：解：设等差数列{an}的公差为d，
    由题意可得a1+4d=2（a1+9d），
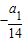
    解得d=＜0，数列递减，
    可得通项公式an=a1+（n-1）d=，
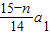
    令an≤0，结合a1＞0可解得n≥15，
    故数列的前14项为正，第15项为0，从第16项开始为负，
    故数列的前14项，或前15项和最大，
    故选D
    点评：本题考查等差数列的前n项和的最值，从数列自身的特点入手是解决问题的关键，属基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1=-2010，其前n项的和为Sn．若
    S2010
    2010
    -
    S2008
    2008
    =2，则S2010=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1+3a8+a15=60，则2a9-a10的值为
    12
    12
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知在等差数列{an}中，d＞0，a2008、a2009是方程x2-3x-5=0的两个根，那么使得前n项和Sn为负值的最大的n的值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，已知a1=2，a2+a3=13，则a4+a5+a6等于=
    42
    42
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，若S4=1，S8=4，则a17+a18+a19+a20的值=
    9
    9
    ．

    查看答案和解析>>

    同步练习册答案