
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源:不详 题型:解答题
| 动作 | K | D | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 | 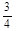 | 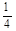 | 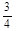 | 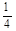 |
| 动作 | K | D | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 | 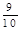 | 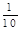 | 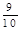 | 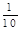 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
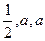 (0<a<1),三各射击一次,击中目标的次数记为
(0<a<1),三各射击一次,击中目标的次数记为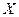 。
。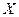 的分布列;
的分布列; 的值最大,求实数a的取值范围。
的值最大,求实数a的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
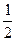 ,x(x>
,x(x>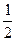 );且乙运动员在2次独立射击中恰有1次命中10环的概率为
);且乙运动员在2次独立射击中恰有1次命中10环的概率为
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
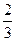 ,
,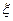 ,求
,求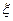 的分布列及数学期望
的分布列及数学期望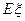 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求 的分布列和期望
的分布列和期望查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com