Question

12．已知球的内接三棱锥D一ABC，△ABC中，AB⊥AC且AB=AC=2$\sqrt{2}$，DB=DC=4，二面角A-BC-D的大小为$\frac{3π}{4}$，若球内一飞行物（忽略其大小）可以在球内任意飞行，则落在三棱锥D-ABC内的概率为（　　）

• A． $\frac{3π}{13}$
• B． $\frac{8\sqrt{2}}{27π}$
• C． $\frac{8}{85π}$
• D． $\frac{9\sqrt{10}}{200π}$

Answer 1

分析 根据球内接三棱锥D一ABC的长度关系，求出球的半径以及三棱锥的体积，根据几何概型的概率公式进行求解即可．

解答 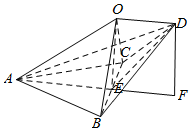解：∵球的内接三棱锥D一ABC，△ABC中，AB⊥AC，
∴取BC的中点E，则E是截面△ABC对应小圆的圆心，
设球心为0，则OE⊥面ABC，
设OE=h，球半径为R，
则OA=OD=OB=R，
∵DB=DC=4，∴DE⊥BC，
∵AB=AC=2$\sqrt{2}$，∴AE⊥BC，
即∠AED是二面角A-BC-D的大小，
即∠AED=$\frac{3π}{4}$，则∠OED=$\frac{3π}{4}$-$\frac{π}{2}$=$\frac{π}{4}$，
∵△ABC中，AB⊥AC且AB=AC=2$\sqrt{2}$，∴AE=2，BC=4，
∵DB=DC=4，∴在正△BCD中，DE=2$\sqrt{3}$，
则OA²=OE²+AE²，
即R²=h²+4  ①
在△OED中，OD²=OE²+DE²-2OE•DEcos$\frac{π}{4}$，
即R²=h²+12-2h×2$\sqrt{3}$×$\frac{\sqrt{2}}{2}$=h²+12-2$\sqrt{6}$h，②
即4+h²=h²+12-2$\sqrt{6}$h，
∴h=$\frac{4}{\sqrt{6}}$，R=$\sqrt{（\frac{4}{\sqrt{6}}）^{2}+4}$=$\sqrt{\frac{40}{6}}$=$\frac{2\sqrt{15}}{3}$，
三棱锥D一ABC的高OF=DE•sin$\frac{π}{4}$=2$\sqrt{3}×\frac{\sqrt{2}}{2}$=$\sqrt{6}$，
则三棱锥D-ABC的体积V=$\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×2\sqrt{2}$×$\sqrt{6}$=$\frac{4\sqrt{6}}{3}$，
球的体积V=$\frac{4}{3}π×$（$\frac{2\sqrt{15}}{3}$）³=$\frac{160\sqrt{15}}{27}$π，
则落在三棱锥D-ABC内的概率为$\frac{\frac{4\sqrt{6}}{3}}{\frac{160\sqrt{15}π}{27}}$=$\frac{9\sqrt{10}}{200π}$，
故选：D

点评 本题主要考查几何概型的概率的计算，根据球内接三棱锥D一ABC的关系求出球的半径和三棱锥的体积是解决本题的关键．综合性较强，难度较大．