
分析 (1)由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式.
(2)由条件利用正弦函数的定义域和值域,求得函数f(x)在区间$[-\frac{3π}{2},0]$上的最值.
解答 解:(1)∵$\frac{T}{2}=3π∴T=6π∴ω=\frac{2π}{T}=\frac{2π}{6π}=\frac{1}{3}$,
$\frac{T}{2}=3π$,∴T=6π,∴$ω=\frac{2π}{T}=\frac{2π}{6π}=\frac{1}{3}$,
又∵A=2,∴$f(x)=2cos(\frac{1}{3}x+ϕ)$.
∵图象过点(0,1),∴2cosϕ=1,∵0<ϕ<π,∴$ϕ=\frac{π}{3}$,
∴$f(x)=2cos(\frac{1}{3}x+\frac{π}{3})$.
(2)∵$-\frac{3}{2}π≤x≤0∴-\frac{π}{6}≤\frac{1}{3}x+\frac{π}{3}≤\frac{π}{3}$,∴$当\frac{1}{3}x+\frac{π}{3}=0即x=-π时,f{(x)_{max}}=2$.$当\frac{1}{3}x+\frac{π}{3}=\frac{π}{3}即x=0时,f{(x)_{min}}=1$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,正弦函数的定义域和值域,属于基础题.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
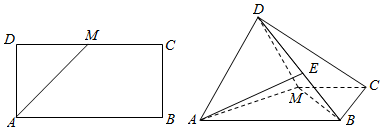
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{13}$ | B. | $\frac{8\sqrt{2}}{27π}$ | C. | $\frac{8}{85π}$ | D. | $\frac{9\sqrt{10}}{200π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或-1 | B. | 2 | C. | -1 | D. | 2或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | EF与BC相交 | B. | EF∥BC | C. | EF与BC异面 | D. | 以上均有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
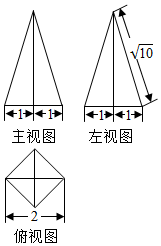 一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )
一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com