Question

8．如图，已知长方形ABCD中，AB=2，AD=1，M为DC的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM，E为BD的中点．

（1）求证：BM⊥平面ADM；
（2）求直线AE与平面ADM所成角的正弦值．

Answer 1

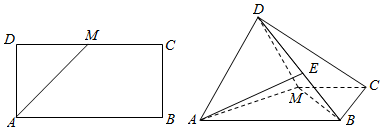
分析 （1）根据线面垂直的判定定理证明即可；（2）求出平面ADM的一个法向量，求出$\overrightarrow{AE}$，$\overrightarrow{MB}$的余弦值，从而求出直线AE与平面ADM所成角的正弦值．

解答 解：（1）△ABM中，AB=2，$AM=BM=\sqrt{2}$，∴AM⊥BM，
又平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，且BM⊆平面ABCM，
∴BM⊥平面ADM…（6分）
（2）如图，以M点为坐标原点，MA所在直线为x轴，MB所在直线为y轴建立空间直角坐标系，
则M（0，0，0），$A（\sqrt{2}，0，0）$，$B（0，\sqrt{2}，0）$，$D（\frac{{\sqrt{2}}}{2}，0，\frac{{\sqrt{2}}}{2}）$，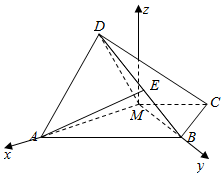


∵E为BD中点，∴$E（\frac{{\sqrt{2}}}{4}，\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{2}}}{4}）$，$\overrightarrow{AE}=（-\frac{{3\sqrt{2}}}{4}，\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{2}}}{4}）$，
由（1）知，$\overrightarrow{MB}$为平面ADM的一个法向量，
$\overrightarrow{MB}=（0，\sqrt{2}，0）$，
$cos＜\overrightarrow{AE}，\overrightarrow{MB}＞=\frac{{\overrightarrow{AE}•\overrightarrow{MB}}}{{|{\overrightarrow{AE}}|•|{\overrightarrow{MB}}|}}=\frac{{\frac{{\sqrt{2}}}{2}×\sqrt{2}}}{{\sqrt{\frac{9}{8}+\frac{1}{2}+\frac{1}{8}}×\sqrt{2}}}=\frac{{\sqrt{14}}}{7}$，
∴直线AE与平面ADM所成角的正弦值为$\frac{{\sqrt{14}}}{7}$…（12分）

点评 本题考查了线面垂直的判定，考查平面的法向量问题，考查线面角问题，是一道中档题．