
分析 (1)由条件利用两个向量的数量积公式,正弦函数的图象的对称性,求得ω的值,可得函数的解析式,再根据函数的图象经过特殊点,求得λ的值,从而得到函数的解析式.
(2)由条件利用同角三角的基本关系求得α、α+β的正弦和余弦,再利用两角差的余弦公式求得cosβ的值,可得β的值.
解答 解:(1)由$f(x)=\overrightarrow a•\overrightarrow b+λ$得$f(x)=2{sin^2}ωx+2\sqrt{3}cosωxsinωx+λ$
=1-cos2ωx+$\sqrt{3}$sin2ωx+λ=2sin(2ωx-$\frac{π}{6}$)+λ+1,
可得 $f(x)=2sin({2ωx-\frac{π}{6}})+λ+1$.
由于函数f(x)的图象关于直线$x=\frac{π}{3}$对称,∴$sin({\frac{2π}{3}ω-\frac{π}{6}})=±1$,
解得:$ω=1+\frac{3}{2}k,k∈Z$,∵ω∈(0,2),∴ω=1.
又因为f(x)经过点$({\frac{π}{4},\sqrt{3}})$,可得:λ=-1,因此$f(x)=2sin({2x-\frac{π}{6}})$.
(2)由$f({\frac{α}{2}+\frac{π}{3}})=\frac{2}{7}⇒cosα=\frac{1}{7},f({\frac{α+β}{2}+\frac{π}{12}})=\frac{{5\sqrt{3}}}{7}⇒sin({α+β})=\frac{{5\sqrt{3}}}{14}$.
∵α为锐角且$cosα=\frac{1}{7}$,∴$sinα=\sqrt{1-{{cos}^2}α}=\frac{{4\sqrt{3}}}{7}$,
又α,β为锐角,∴$α+β∈({\frac{π}{2},π})$,
又$sin({α+β})=\frac{{5\sqrt{3}}}{14}<sinα$,∴$α+β∈({\frac{π}{2},π})$,∴$cos({α+β})=\sqrt{1-{{sin}^2}({α+β})}=-\frac{11}{14}$,
∴$cosβ=cos[{({α+β})-α}]=cos({α+β})cosα+sin({α+β})sinα=\frac{1}{2}$,∴$β=\frac{π}{3}$.
点评 本题主要考查两个向量的数量积公式,正弦函数的图象的对称性,同角三角的基本关系,两角差的余弦公式,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
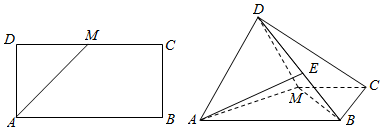
| A. | EF与BC相交 | B. | EF∥BC | C. | EF与BC异面 | D. | 以上均有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | [$\frac{1}{4},\frac{1}{2}$) | C. | ($\frac{1}{4},\frac{1}{2}$) | D. | ($0,\frac{1}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
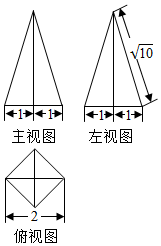 一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )
一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1-$\sqrt{2}$,0] | B. | [0,$\sqrt{2}$+1] | C. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | D. | [1,$\sqrt{2}$+1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com