
分析 通过题意可知a=$\frac{1}{bc}$、b=$\frac{1}{ac}$、c=$\frac{1}{ab}$,进而$\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$=$\sqrt{\frac{1}{b}•\frac{1}{c}}$+$\sqrt{\frac{1}{a}•\frac{1}{c}}$+$\sqrt{\frac{1}{a}•\frac{1}{b}}$,利用基本不等式计算即得结论.
解答 证明:依题意,a=$\frac{1}{bc}$、b=$\frac{1}{ac}$、c=$\frac{1}{ab}$,
∴$\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$=$\sqrt{\frac{1}{bc}}$+$\sqrt{\frac{1}{ac}}$+$\sqrt{\frac{1}{ab}}$
=$\sqrt{\frac{1}{b}•\frac{1}{c}}$+$\sqrt{\frac{1}{a}•\frac{1}{c}}$+$\sqrt{\frac{1}{a}•\frac{1}{b}}$
<$\frac{1}{2}$($\frac{1}{b}$+$\frac{1}{c}$)+$\frac{1}{2}$($\frac{1}{a}$+$\frac{1}{c}$)+$\frac{1}{2}$($\frac{1}{b}$+$\frac{1}{a}$)
=$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$.
点评 本题考查不等式的证明,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.


 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
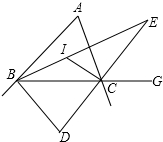 好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决,如图,在ABC中,∠BAC=50°,点I是两角B、C平分线的交点.
好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决,如图,在ABC中,∠BAC=50°,点I是两角B、C平分线的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
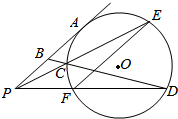 如图,过点P作⊙O的切线PA,A为切点,过PA中点B作割线交⊙O于C、D,连结PC并延长⊙O于E,连结PD,交⊙O于F,求证:EF∥PA.
如图,过点P作⊙O的切线PA,A为切点,过PA中点B作割线交⊙O于C、D,连结PC并延长⊙O于E,连结PD,交⊙O于F,求证:EF∥PA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P<R<Q | B. | R<Q<P | C. | R<P<Q | D. | Q<R<P |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com