
 高一某研究性学习小组随机抽取了100名年龄在10岁到60岁的市民进行问卷调查,并制作了频率分布直方图(如图),从图中数据可知a=0.035.现从上述年龄在20岁到50岁的市民中按年龄段采用分层抽样的方法抽取30人,则在[20,30)年龄段抽取的人数应为10.
高一某研究性学习小组随机抽取了100名年龄在10岁到60岁的市民进行问卷调查,并制作了频率分布直方图(如图),从图中数据可知a=0.035.现从上述年龄在20岁到50岁的市民中按年龄段采用分层抽样的方法抽取30人,则在[20,30)年龄段抽取的人数应为10. 分析 根据频率和为1,列出方程求出a的值;利用分层抽样原理,求出在[20,30)年龄段内的人数与20~50内的人数,即可计算应抽取的人数.
解答 解:根据频率和为1,得10a=1-(0.020+0.025+0.015+0.005),
解得a=0.035;
又市民年龄在20~50岁的人数为100×(1-0.020×10-0.005×10)=75,
且在[20,30)年龄段内的人数是100×0.025×10=25,
则采用分层抽样的方法抽取30人,在[20,30)年龄段抽取的人数应为
30×$\frac{25}{75}$=10.
故答案为:0.035,10.
点评 本题考查了频率分布直方图的应用问题,也考查了分层抽样方法的应用问题,是基础题目.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
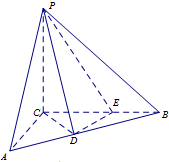 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$,D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2,AC=$\frac{3}{2}$.
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$,D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2,AC=$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10$\sqrt{3}$nmile | B. | $\frac{10\sqrt{6}}{3}$nmile | C. | 5$\sqrt{2}$nmile | D. | 5$\sqrt{6}$nmile |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,2] | C. | (2,+∞) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥O-ABCD中,底面ABCD是矩形,
在四棱锥O-ABCD中,底面ABCD是矩形,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com