
【题目】已知函数![]() (其中
(其中![]() ,
,![]() ,
,![]() ,
,![]() 是实数常数,
是实数常数,![]() ).
).
(1)若![]() ,函数
,函数![]() 的图象关于点
的图象关于点![]() 成中心对称,求
成中心对称,求![]() ,
,![]() 的值;
的值;
(2)若函数![]() 满足条件(1),且对任意
满足条件(1),且对任意![]() ,总有
,总有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() 是奇函数,
是奇函数,![]() ,
,![]() ,且对任意
,且对任意![]() 时,不等式
时,不等式![]() 恒成立,求负实数
恒成立,求负实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)将![]() 化为
化为![]() ,类比
,类比![]() 的图象得对称中心
的图象得对称中心![]() ,对应相等可求得结果;(2)整理可得:
,对应相等可求得结果;(2)整理可得:![]() ;当
;当![]() 时符合题意;
时符合题意;![]() 时由单调性可知不合题意;当
时由单调性可知不合题意;当![]() 时,可知只需
时,可知只需![]() ,从而得到
,从而得到![]() 的范围;综合三种情况得到结果;(3)根据奇偶性和函数值可得:
的范围;综合三种情况得到结果;(3)根据奇偶性和函数值可得:![]() ,根据
,根据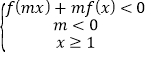 得到
得到![]() ,根据单调性求解出
,根据单调性求解出![]() 的最小值,则根据
的最小值,则根据![]() 求得结果.
求得结果.
(1)![]()
![]()
类比函数![]() 的图象,可知函数
的图象,可知函数![]() 的图象的对称中心是
的图象的对称中心是![]()
又![]() 函数
函数![]() 的图象的对称中心
的图象的对称中心![]()
![]()
(2)由(1)知,![]()
依据题意,对任意![]() ,恒有
,恒有![]() .
.
①当![]() 时,
时,![]() ,符合题意
,符合题意
②当![]() 时,对任意
时,对任意![]() ,则
,则![]()
恒有![]() ,不符合题意;
,不符合题意;
③当![]() 时,函数
时,函数![]() 在
在![]() 上是单调递减函数,且满足
上是单调递减函数,且满足![]()
因此,只需![]() 即可
即可
解得:![]()
综上所述,实数![]() 的范围
的范围![]()
(3)依据题设: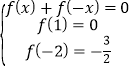 ,解得:
,解得: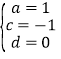
于是![]()
由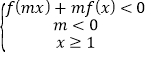 ,得
,得![]() ,
,
![]()
![]()
![]()
因此![]()
![]() 函数
函数![]() 在
在![]() 是增函数
是增函数
![]() .
.
![]() 所求负实数
所求负实数![]() 的取值范围
的取值范围![]()


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
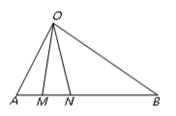
【题目】如图所示,某公路![]() 一侧有一块空地
一侧有一块空地![]() ,其中
,其中 ![]() ,
,![]() .当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
.当地政府拟在中间开挖一个人工湖△OMN,其中M,N都在边AB上(M,N不与A,B重合,M在A,N之间),且∠MON=30°.
(1)若M在距离A点2 km处,求点M,N之间的距离;
(2)为节省投入资金,人工湖△OMN的面积要尽可能小.试确定M的位置,使△OMN的面积最小,并求出最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=5,a5﹣2a2=3,又等比数列{bn}中,b1=3且公比q=3.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若cn=an+bn , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x+2|﹣|x﹣1|
(I)画出函数y=f(x)的图象;
(II)若关于x的不等式f(x)+4≥|1﹣2m|有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解放军某部在实兵演练对抗比赛中,红、蓝两个小组均派6人参加实弹射击,其所得成绩的茎叶图如图所示.
(1)根据射击数据,计算红、蓝两个小组射击成绩的均值与方差,并说明红军还是蓝军的成绩相对比较稳定;
(2)若从蓝军6名士兵中随机抽取两人,求所抽取的两人的成绩之差不超过2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过点A作AD⊥CD于D,交半圆于点E,DE=1.
(Ⅰ)求证:AC平分∠BAD;
(Ⅱ)求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3ax(a∈R)
(1)当a=1时,求f(x)的极小值;
(2)若直线x+y+m=0对任意的m∈R都不是曲线y=f(x)的切线,求a的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).

(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com