
分析 由题意和同角三角函数基本关系可得sinα和cosα,代入两角差的余弦公式计算可得.
解答 解:∵α为锐角,∴sinα>0,
又∵3sinα=tanα,∴3sinα=$\frac{sinα}{cosα}$,
∴约掉sinα可得cosα=$\frac{1}{3}$,
∴sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{2\sqrt{2}}{3}$,
∴cos(α-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$cosα+$\frac{\sqrt{2}}{2}$sinα
=$\frac{\sqrt{2}}{2}$×$\frac{1}{3}$+$\frac{\sqrt{2}}{2}$×$\frac{2\sqrt{2}}{3}$=$\frac{4+\sqrt{2}}{6}$.
故答案为:$\frac{4+\sqrt{2}}{6}$.
点评 本题考查两角和与差的余弦公式和同角三角函数基本关系,属基础题.


科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①②④ | C. | ①④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$或$\sqrt{2}$ | D. | 3-$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
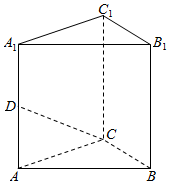 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,BC=1,$∠BAC=\frac{π}{6}$,D为棱AA1中点,证明异面直线B1C1与CD所成角为$\frac{π}{2}$,并求三棱柱ABC-A1B1C1的体积.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,BC=1,$∠BAC=\frac{π}{6}$,D为棱AA1中点,证明异面直线B1C1与CD所成角为$\frac{π}{2}$,并求三棱柱ABC-A1B1C1的体积.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{2}$)∪($\sqrt{2}$,+∞) | B. | ($\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
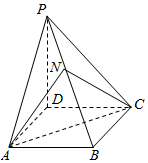 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:6 | D. | 1:8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com