
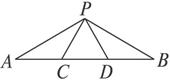
图1-3-17
(1)当AC、CD、DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.
思路分析:本题是一个探索型的问题,考查相似三角形的判定及性质,它给出了一个条件,让你自己再添加一个条件,可使两个三角形相似.因此,首先想到相似的判定方法,因又限制了三条边的关系,所以是对应边就成比例.当三角形相似以后,那么对应角相等,易求∠APB.
解:(1)∵△PCD是等边三角形,
∴∠PCD=∠PDC=60°,PD=PC=CD.
从而∠ACP=∠PDB=120°.
∴当![]() 时,△ACP∽△PDB.
时,△ACP∽△PDB.
即当CD2=AC·BD时,△ACP∽△PDB.
(2)当△ACP∽△PDB时,∠APC=∠PBD.
∴∠APB=∠APC+∠CPD+∠DPB
=∠PBD+60°+∠DPB
=60°+60°=120°.


科目:高中数学 来源: 题型:
地面上有一旗杆OP,如图1-2(3)-17,为了测得它的高度,在地面上选一基线AB,测得AB=20 m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=60°,求旗杆的高度.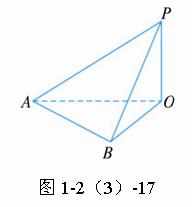
查看答案和解析>>
科目:高中数学 来源: 题型:
地面上有一旗杆OP,如图1-2(3)-17,为了测得它的高度,在地面上选一基线AB,测得AB=

查看答案和解析>>
科目:高中数学 来源: 题型:
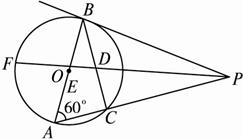
图2-4-17
(1)求证:PA·BD=PB·AE;
(2)证明⊙O的直径长为常数;
(3)求tan∠FPA的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com