【题目】已知A、B是抛物线W： 
上的两个动点，F是抛物线W的焦点， 
是坐标原点，且恒有
.
(1)若直线OA的倾斜角为
时，求线段AB的中点C的坐标；
(2)求证直线AB经过一定点，并求出此定点.
【答案】（1）中点C（
）（2）定点坐标
【解析】试题分析:(1)由点斜式写出直线OA 方程,与抛物线方程联立解得A点坐标，由
得直线OB的倾斜角为
，由点斜式写出直线OB方程,与抛物线方程联立解得B点坐标，最后根据中点坐标公式得 AB的中点C的坐标；(2)先设直线OA的斜率，由点斜式写出直线OA 方程,与抛物线方程联立解得A点坐标，由
得直线OB的斜率，由点斜式写出直线OB方程,与抛物线方程联立解得B点坐标，根据两点式得AB方程，根据方程求出定点坐标
试题解析:（1）OA: 
,所以由
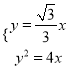得
因为
，所以OB: 
,所以由
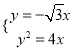得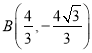
因此线段AB的中点C的坐标为（
）
（2）设OA: 
,所以由
得
因为
，所以OB: 
,所以由
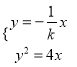得
所以AB: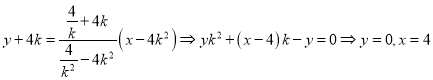 
因此直线AB经过一定点
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】在△ABC中，内角A、B、C的对边分别为a，b，c，且2asinB﹣ 
bcosA=0．
（1）求cosA；
（2）若a= ，b=2，求△ABC的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将A、B两枚骰子各抛掷一次，观察向上的点数，问：
（1）共有多少种不同的结果？
（2）两枚骰子点数之和是3的倍数的结果有多少种？
（3）两枚骰子点数之和是3的倍数的概率为多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业节能降耗技术改造后，在生产某产品过程中几录的产量x（吨）与相应的生产能耗y（吨）的几 组对应数据如表所示：
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | a |
若根据表中数据得出y关于x的线性回归方程为 
=0.7x+0.35，则表中a的值为（ ）
A.3
B.3.15
C.3.5
D.4.5
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2， 
．
（1）把圆O1和圆O2的极坐标方程化为直角坐标方程；
（2）求经过两圆交点的直线的极坐标方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线C1的极坐标方程为ρcos（θ﹣ 
）=﹣1，曲线C2的极坐标方程为ρ=2 
cos（θ﹣ 
）．以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系．
（1）求曲线C2的直角坐标方程；
（2）求曲线C2上的动点M到曲线C1的距离的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知奇函数f（x）是定义在（﹣2，2）上的减函数，则不等式f（ 
）+f（2x﹣1）＞0的解集是（ ）
A.（﹣∞， 
）
B.[﹣ 
，+∞）
C.（﹣6，﹣ ）
D.（﹣ ， ）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知点A（0，2），B（4，6）， 
=t1 
+t2 
，其中t1、t2为实数；
（1）若点M在第二或第三象限，且t1=2，求t2的取值范围；
（2）求证：当t1=1时，不论t2为何值，A、B、M三点共线；
（3）若t1=a2 ， ⊥ ，且△ABM的面积为12，求a和t2的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
