
(1)已知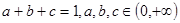 ,求证:
,求证: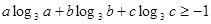 ;
;
(2)已知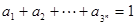 ,
,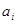 >0(i=1,2,3,…,3n),求证:
>0(i=1,2,3,…,3n),求证:
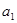
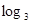
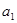 +
+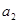
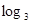
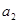 +
+
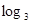
 +…+
+…+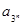
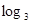
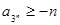
(1)利用函数的单调性,alog3a+blog3b+clog3c≥-1当a=b=c= 时等号成立。
时等号成立。
(2)证明:数学归纳法
【解析】
试题分析:(1)证明: a+b+c=1,a、b、c∈(0,+∞),
a+b+c=1,a、b、c∈(0,+∞),
alog3a+blog3b+clog3c= alog3a+blog3b+(1-a-b) log3(1-a-b)="f(a)"
那么f ′ (a)= log3a-log3(1-a-b),当a∈(0, )时f ′ (a)<0,当a∈(
)时f ′ (a)<0,当a∈( ,1)时f ′ (a)>0,
,1)时f ′ (a)>0,
f(a)在(0, ]上递减,在[
]上递减,在[ ,1) 上递增;
,1) 上递增;
f(a)≥f( )="(1-b)" log3
)="(1-b)" log3 + blog3b,记g(b)="
(1-b)" log3
+ blog3b,记g(b)="
(1-b)" log3 + blog3b, 3分
+ blog3b, 3分
得:g′(b)= log3b-log3 ,当b∈(0,
,当b∈(0, )时g′(b) <0,当b∈(
)时g′(b) <0,当b∈( ,1)时,g′(b) >0,
,1)时,g′(b) >0,
 g(b)在(0,
g(b)在(0, )递减,在(
)递减,在( ,1)上递增;
,1)上递增; g(b)≥g(
g(b)≥g( )=-1。
)=-1。
alog3a+blog3b+clog3c≥-1当a=b=c= 时等号成立。5分
时等号成立。5分
(2)证明:n=1时, +
+ +
+ =1,
=1, >0(i=1,2,3),由(1)知
>0(i=1,2,3),由(1)知


 +
+

 +
+

 ≥-1成立,即n=1时,结论成立。
≥-1成立,即n=1时,结论成立。
设n=k时结论成立,即 +
+ +…+
+…+ =1,
=1, >0(i=1,2,3,…,3k)时
>0(i=1,2,3,…,3k)时


 +
+

 +
+

 +…+
+…+

 ≥-k.
≥-k.
那么,n=k+1时,若 +
+ +…+
+…+ +
+ +…+
+…+ =1,
=1, >0(i=1,2,3,…,3k+1)时,
>0(i=1,2,3,…,3k+1)时,
令 +…+
+…+ =t,则
=t,则 +
+ +…+
+…+ =1,由归纳假设:
=1,由归纳假设:


 +
+

 +…+
+…+

 ≥-k. 8分
≥-k. 8分



 +
+

 +
+

 +…+
+…+

 -(1-t)
-(1-t)  (1-t) ≥-k(1-t).
(1-t) ≥-k(1-t).



 +
+

 +
+

 +…+
+…+

 ≥-k(1-t)+ (1-t)
≥-k(1-t)+ (1-t)  (1-t)…(1)
(1-t)…(1)
设 +…+
+…+ =s,则
=s,则 +…+
+…+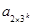 =t-s,
=t-s, +
+ +…+
+…+ =1,
=1,
由归纳假设:

 +
+

 +…+
+…+

 ≥-k.
≥-k.



 +
+

 +…+
+…+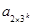

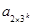 ≥-k(t-s)+ (t-s)
≥-k(t-s)+ (t-s) (t-s)
(t-s)
………(2) 10分

 +…+
+…+ =s,
=s,
 +
+ +…+
+…+ =1;由归纳假设同理可得:
=1;由归纳假设同理可得:


 +
+

 +…+
+…+

 ≥-ks+ s
≥-ks+ s s ……(3)
s ……(3)
将(1) 、(2)、(3)两边分别相加得:


 +
+

 +…+
+…+

 +…+
+…+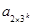

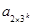 +…+
+…+


≥-k[(1-t)+(t-s)+s]+ (1-t) (1-t)+ (t-s)
(1-t)+ (t-s) (t-s) + s
(t-s) + s s
s
而(1-t)+(t-s)+s=1,(1-t)>0,(t-s) >0,s >0。 (1-t)
(1-t) (1-t)+ (t-s)
(1-t)+ (t-s) (t-s) + s
(t-s) + s s≥-1。
s≥-1。
 -k[(1-t)+(t-s)+s]+
(1-t)
-k[(1-t)+(t-s)+s]+
(1-t) (1-t)+ (t-s)
(1-t)+ (t-s) (t-s) + s
(t-s) + s s≥-k-1=-(k+1)。
s≥-k-1=-(k+1)。



 +
+

 +…+
+…+

 +…+
+…+

 ≥-(k+1)。
≥-(k+1)。
 n=k+1时,题设结论成立。综上所述,题设结论得证。 13分
n=k+1时,题设结论成立。综上所述,题设结论得证。 13分
考点:本题主要考查对数函数的性质,函数的单调性,数学归纳法证明不等式。
点评:难题,利用已知a,b,c的关系,首先确定得到函数f(a),从而利用导数研究函数的单调性,达到证明不等式的目的。(2)利用数学归纳法证明不等式,看似思路清晰,但在不等式变形过程中,困难重重。是一道比较难的题目。


科目:高中数学 来源: 题型:
| π |
| 3 |
| C |
| 2 |
| A |
| 2 |
| 3b |
| 2 |
| 1+sin2B |
| cosB+sinB |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
|
|
| 1+x2 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)求实数λ的取值范围,使不等式|![]() |>1对满足|a|<1,|b|<1的一切实数a、b恒成立;
|>1对满足|a|<1,|b|<1的一切实数a、b恒成立;
(3)已知|a|<1,若|![]() |<1,求b的取值范围.
|<1,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年吉林省高一下学期期中考试数学 题型:解答题
△ABC的三个内角A、B、C的对边的长分别为a、b、c,有下列两个条件:(1)a、b、c成等差数列;(2)a、b、c成等比数列,现给出三个结论:(1)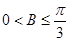 ;(2)
;(2)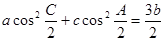 ;(3)
;(3)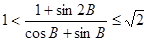 。
。
请你选取给定的两个条件中的一个条件为条件,三个结论中的两个为结论,组建一个你认为正确的命题,并证明之。
(I)组建的命题为:已知_______________________________________________
求证:①__________________________________________
②__________________________________________
(II)证明:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com