
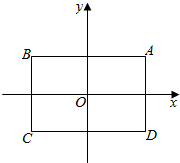
 ��ͼ������ԭ��OΪ����ABCD�ĶԳ����ģ�����A������Ϊ��1��t����AB��x�ᣬ����A��B��C��D�������ABCD��λ��ͼ�Σ���OΪλ�����ģ���A�䣬B����ǵ�A��B�Ķ�Ӧ�㣬$\frac{A��B��}{AB}$=k����֪����x��y��Ԫ����һ�η���$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$��m��n��ʵ�����⣬����m��nΪ���꣨��Ϊm��n�������еĵ��У�������ֻ��һ�������ھ���A��B��C��D��ı��ϣ���k•t��ֵ����1��
��ͼ������ԭ��OΪ����ABCD�ĶԳ����ģ�����A������Ϊ��1��t����AB��x�ᣬ����A��B��C��D�������ABCD��λ��ͼ�Σ���OΪλ�����ģ���A�䣬B����ǵ�A��B�Ķ�Ӧ�㣬$\frac{A��B��}{AB}$=k����֪����x��y��Ԫ����һ�η���$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$��m��n��ʵ�����⣬����m��nΪ���꣨��Ϊm��n�������еĵ��У�������ֻ��һ�������ھ���A��B��C��D��ı��ϣ���k•t��ֵ����1�� ���� �����Ʊ�Ϊk�����A�������Ϊ��k��kt�������ݹ���x��y��Ԫ����һ�η���$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$��m��n��ʵ�����⣬�ɵã�mn=3��n��1��������ֻ��һ�������ھ���A��B��C��D��ı��ϣ����ݷ����������ĶԳ��ԣ��ɵ÷���������n=$\frac{3}{m}$��n��1����ͼ��ֻ������C�䣬��A��������Ϊ��3��1���������õ��𰸣�
��� �⣺����A��B��C��D�������ABCD��λ��ͼ�Σ�
�����Ʊ�Ϊk��
����A��������1��t����
���A���������k��kt����
�߹���x��y��Ԫ����һ�η���$\left\{\begin{array}{l}{mnx+y=3n+1}\\{3x+y=4}\end{array}\right.$��m��n��ʵ�����⣬
��mn=3��n��1��
����m��nΪ���꣨��Ϊm��n�������еĵ��У�������ֻ��һ�������ھ���A��B��C��D��ı��ϣ�
�෴��������n=$\frac{3}{m}$��ͼ��ֻ������A��͵�C�䣬
������������n=$\frac{3}{m}$��n��1����ͼ��ֻ������C�䣬
��A����������3��1����
��k•t=1��
�ʴ�Ϊ��1��
���� ���⿼���֪ʶ���Ƿ����������ĶԳ��ԣ�һԪ���η��̸��ĸ����жϣ�λ��ͼ�Σ��dz���֪ʶ���ۺ�Ӧ�ã��Ѷ��е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com