
分析 (1)将圆的方程化为标准方程,可得圆心坐标,再消去参数,即可得到结论;
(2)设与l平行的直线是l1:x-3y+b=0,求出圆心到直线l1的距离,与半径比较,即可得出结论;
(3)设出与直线?平行的直线的方程:x-3y+b=0,利用点到直线的距离公式表示出圆心到此直线的距离整理后发现不含有参数b,故可得结论.
解答 (1)证明:配方得:(x-3m)2+[y-(m-1)]2=25,设圆心为(x,y),
则$\left\{\begin{array}{l}{x=3m}\\{y=m-1}\end{array}\right.$,
消去m得x-3y-3=0,则圆心恒在直线l:x-3y-3=0上.
(2)解:设与l平行的直线是l1:x-3y+b=0,
则圆心到直线l1的距离为d=$\frac{|3m-3(m-1)+b|}{\sqrt{10}}$=$\frac{|3+b|}{\sqrt{10}}$.
∵圆的半径为r=5,
∴当d<r,即-5$\sqrt{10}$-3<b<5$\sqrt{10}$-3时,直线与圆相交;
当d=r,即b=±5$\sqrt{10}$-3时,直线与圆相切;
当d>r,即b<-5$\sqrt{10}$-3或b>5$\sqrt{10}$-3时,直线与圆相离.
(3)证明:对于任一条平行于l且与圆相交的直线l1:x-3y+b=0,由于圆心到直线l1的距离d=$\frac{|3+b|}{\sqrt{10}}$,
弦长=2$\sqrt{{r}^{2}}-{d}^{2}$且r和d均为常量.
∴任何一条平行于l且与圆相交的直线被各圆截得的弦长相等.
点评 本题考查直线与圆的方程的应用,考查弦长的计算,考查学生的计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∈l,A∈α,B∈l,B∈α⇒l?α | B. | A∈α,A∈β,B∈α,B∈β⇒α∩β=AB | ||
| C. | l?α,A∈l⇒A∉α | D. | A∈l,l?α⇒A∈α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 12 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
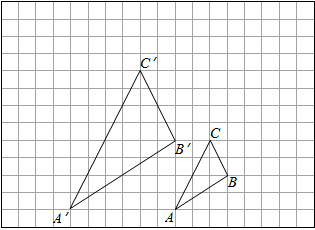 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com