
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 确定f(x)的周期为3,函数在(0,e)上单调递增,在(e,3)上单调递减,在[0,9]上作出y=f(x)的图象,作出y=$\frac{x}{6}$的图象,即可得出结论.
解答 解:当x>0时,f(-x)+f(x+3)=0,∴f(x+3)=-f(-x),
∵f(x)是奇函数,
∴f(x)的周期为3,
当x∈(0,3)时,f(x)=$\frac{elnx}{x}$,∴f′(x)=$\frac{e(1-lnx)}{{x}^{2}}$,
∴函数在(0,e)上单调递增,在(e,3)上单调递减,
在[0,9]上作出y=f(x)的图象,作出y=$\frac{x}{6}$的图象,如图所示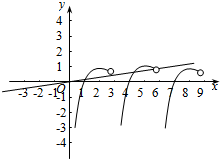
∴在[0,9]上,有3个交点,由对称性,可得方程6f(x)-x=0在[-9,9]上的解的个数为6,
还有f(0)=0,共7个.
故选:D.
点评 本题考查单调性和极值,函数的奇偶、周期性,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
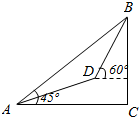 某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为$500(\sqrt{3}+1)$m.
某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为$500(\sqrt{3}+1)$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 应该取消 | 应该保留 | 无所谓 | |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 600人 | x人 | z人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是增函数且最小值为5 | B. | 是增函数且最大值为5 | ||
| C. | 是减函数且最小值为5 | D. | 是减函数且最大值为5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com