
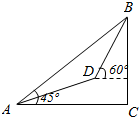
 某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为$500(\sqrt{3}+1)$m.
某登山队在山脚A处测得山顶B的仰角为45°,沿倾斜角为30°的斜坡前进1000m后到达D处,又测得山顶的仰角为60°,则山的高度BC为$500(\sqrt{3}+1)$m. 分析 过点D作DE⊥AC,△ACB是等腰直角三角形,直角△ADE中满足解直角三角形的条件.在直角△BDF中,根据三角函数可得BF,进一步得到BC,即可求出山高.
解答  解:过D分别作DE⊥AC与E,DF⊥BC于F.
解:过D分别作DE⊥AC与E,DF⊥BC于F.
∵在Rt△ADE中,AD=1000m,∠DAE=30°,
∴DE=$\frac{1}{2}$AD=500m.
∵∠BAC=45°,
∴∠DAB=45°-30°=15°,∠ABC=90°-45°=45°.
∵在Rt△BDF中,∠BDF=60°,
∴∠DBF=90°-60°=30°,
∴∠DBA=45°-30°=15°,
∵∠DAB=15°,
∴∠DBA=∠DAB,
∴BD=AD=1000m,
∴在Rt△BDF中,BF=$\frac{\sqrt{3}}{2}$BD=500$\sqrt{3}$m,
∴山的高度BC为$500(\sqrt{3}+1)$m.
故答案为:$500(\sqrt{3}+1)$.
点评 本题考查了解直角三角形的应用-仰角俯角问题的应用,根据已知得出FC,BF的长是解题关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:填空题
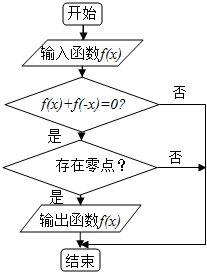 某程序框图如图所示,现输入如下四个函数,其中可以输出的函数是f(x)=sinx.
某程序框图如图所示,现输入如下四个函数,其中可以输出的函数是f(x)=sinx.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
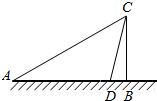 如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )| A. | 50($\sqrt{3}$+1)m | B. | 50($\sqrt{2}$+1)m | C. | 50($\sqrt{3}$-1)m | D. | 50($\sqrt{3}$+$\sqrt{2}$) m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∈l,A∈α,B∈l,B∈α⇒l?α | B. | A∈α,A∈β,B∈α,B∈β⇒α∩β=AB | ||
| C. | l?α,A∈l⇒A∉α | D. | A∈l,l?α⇒A∈α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com